Дифференцируемость функции на числовой оси, уравнения касательных - задачи

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ – 2.

1.  Выбрать функцию g(x) таким образом, чтобы функция , была дифференцируема на всей числовой оси, если

1) 

2) 

3) 

Ö

Ö

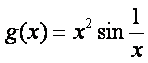
4) 

5)  верного ответа нет

2.  Найти тангенс угла между прямой  и линией

Ответ:  (Комментарий: в случае необходимости ответ записывается обычной дробью).

3.  Найти a и b таким образом, чтобы угол между кривыми  и  в точке x=-1, был равен .

Ответ:  

4.  Для кривой      выбрать среди предложенных такую функцию, чтобы в точке  угол между ними был равен

5.  В какой точке касательная к кривой  параллельна прямой  ().

Ответ:

6. 

Ö

Выбрать среди предложенных равенств уравнения касательных к кривой  в точке