Пример f(x)=x, x [-П, П], Т=2П
1) Построим график функции
2) Проверим условия Дирихле по графику:
а) f(x) монотонна на [-П, П]=Т
б) f(x) непрерывна на [-П, П]=Т
Условия Дирихле выполняется, значит функция разложена в ряд Фурье.
3) функция общего вида, поэтому ряд Фурье имеет вид:
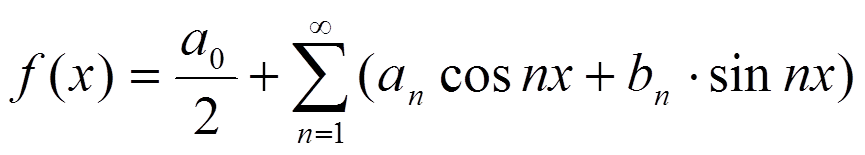
4) Находим коэффициенты
ряда ![]()
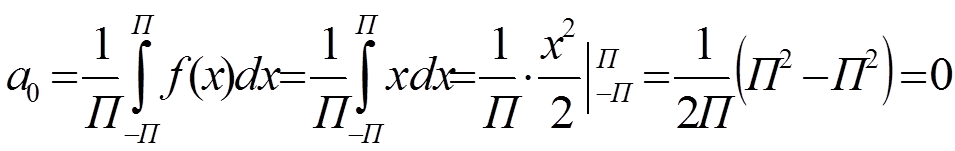
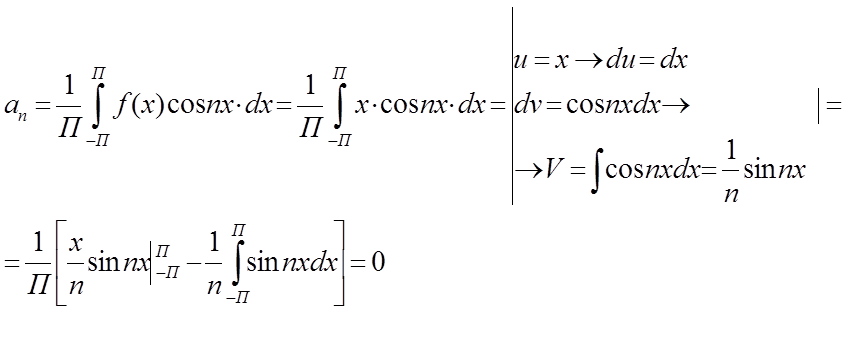
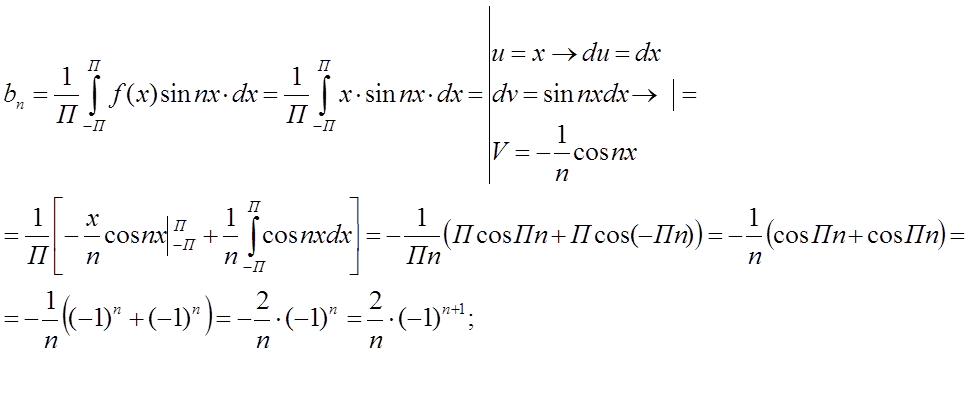
cos 0=1
cos Пn=(-1)n
5) Записываем ряд Фурье
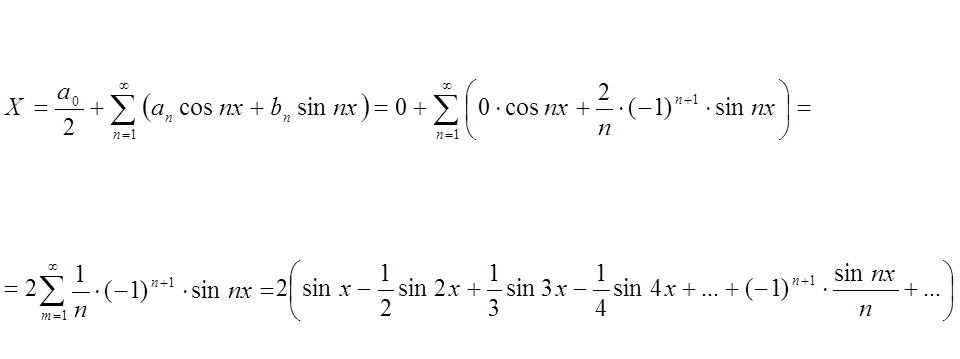
В точке x=-П и x=П сумма ряда Фурье по теореме Фирихле не совпадает со значением функции f(x)=x, а равна
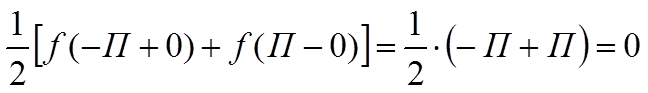
Разложение в ряд фурье четных и нечетных функций с Т=2П
Отметим некоторые свойства четных и нечетных функций:
1) если f(x) и ![]() (x)-четные, то
(x)-четные, то ![]() -четная
функция
-четная
функция
2) если f(x)-четная, ![]() (x)-нечетная, то
(x)-нечетная, то![]() -нечетная
функция
-нечетная
функция
3) если f(x) и ![]() (x)-нечетные, то
(x)-нечетные, то![]() -четная
функция
-четная
функция
4) 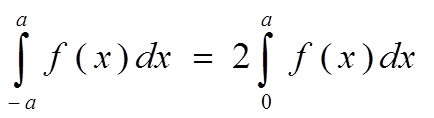 -четная
-четная
5) 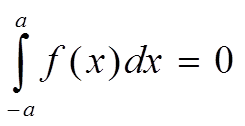 -нечетная
-нечетная
I Пусть f(x)-четная, периодическая функция с периодом Т=2П
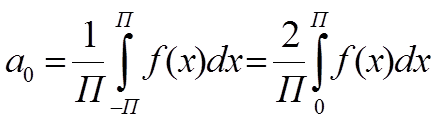 -четная
-четная
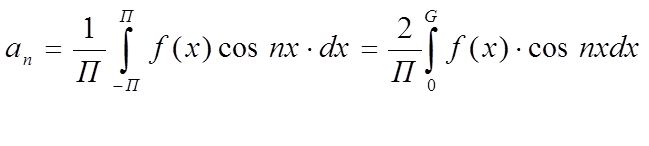 -четная
-четная
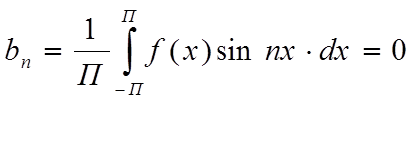 -нечетная
-нечетная
Тогда ряд Фурье имеет вид:
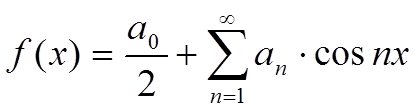
II f(x)-нечетная функция
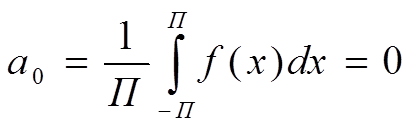 -нечетная
-нечетная
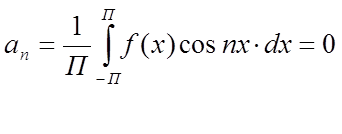 -нечетная
-нечетная
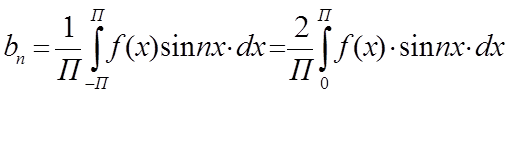 -четная
-четная
ряд Фурье имеет вид:
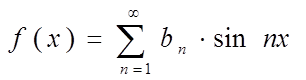
Пример: f(x)=x2. периодическая с Т=2П
1)Построим график функции
2) Проверим условие Фирихле по графику:
а) функция кусочно-монотонная на [-П, П],
б) функция непрерывна на [-П, П]
Значит функция разложима в ряд Фурье.
3)Функция четная 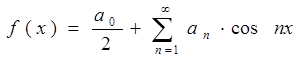
4) Найдем коэффициенты ряда:

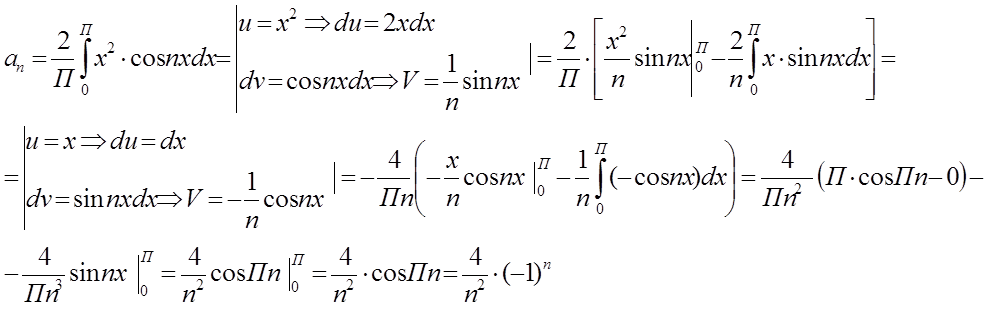 5) Запишем ряд Фурье.
5) Запишем ряд Фурье.
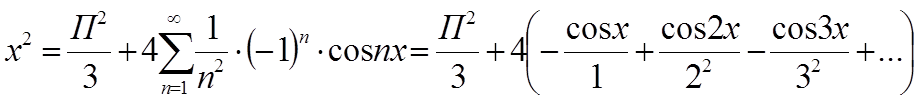
та как функция кусочно-монотонная, непрерывная, то это равенство выполняется во всех точках.
Разложение в ряд Фурье функции с периодом Т=2L
Пусть функция f(x) периодическая с Т=2L, которая на [-L, L] удовлетворяет условием Дарихле, то
мы полагаем 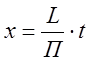 и получим функцию
и получим функцию 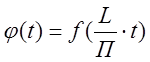 периода 2П
периода 2П
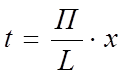
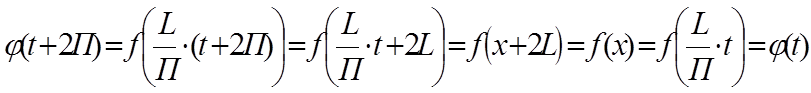 ,
,
которая на [-П, П] удовлетворяет условиям Дирихле. Поэтому в [-П, П]
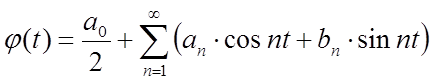 , где
, где 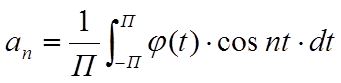
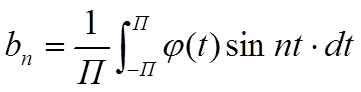
Вернемся к прежней переменной x, получим, что в [-L, L]
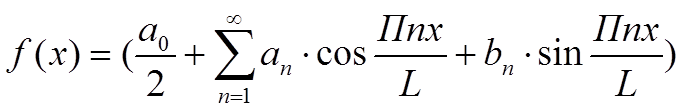 , где
, где
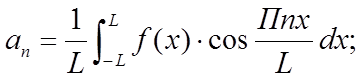
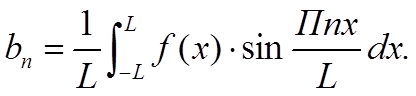
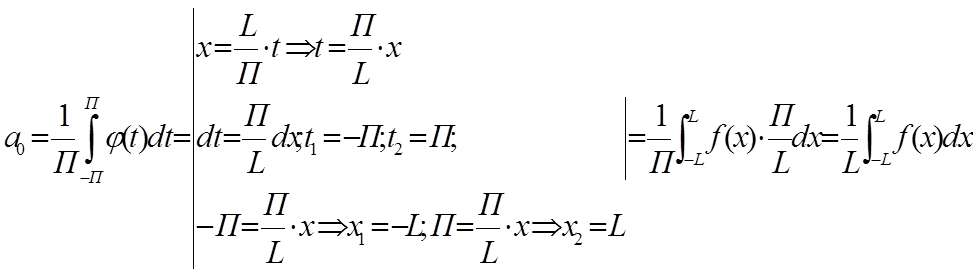
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.