Анализ электрических процессов в цепях второго порядка с последующим построением графиков напряжения на конденсаторе и тока в цепи

После замены, получаем систему дифференциальных уравнений:

Решение полученной системы дифференциальных уравнений в MathCad   имеет вид:

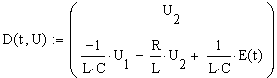
Решение такого уравнения является целью данной курсовой работы.

Для реализации решения данной задачи в MatLab можно использовать решение дифференциального уравнения второго порядка при помощи пакета Simulink и сбора рабочей схемы электрической цепи при помощи пакета SimPowerSystems.

Для реализации данной задачи при помощью пакета Simulink, необходимо вначале собрать схему исследования, рисунок 6. Затем решить дифференциальное уравнение  при помощи блока DEE, рисунок 7.

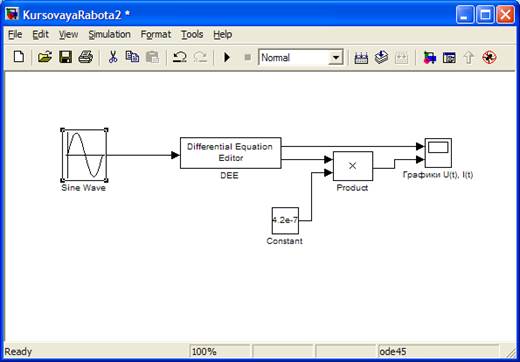
Рисунок 6 - Схема исследования

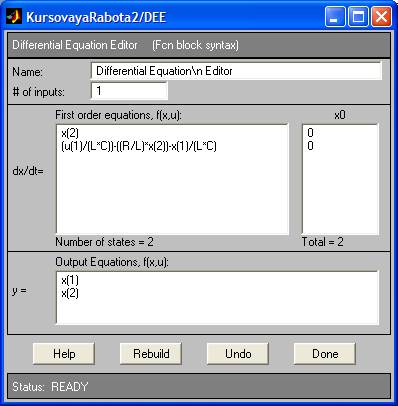
Рисунок 7 – Блок DEE

Для реализации данной задачи при помощью пакета SimPowerSystems, необходимо собрать рабочую схему электрической цепи, рисунок 8.

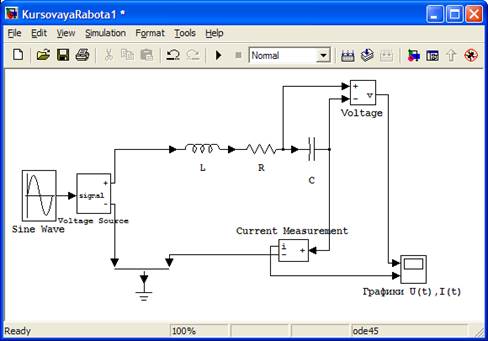
Рисунок 8 - Рабочая схема электрической цепи

3.2 Описание исследований

После решения уравнения: , получим матрицу состоящую из трех столбцов, где первый столбец – это изменение времени t, второй – изменение напряжения  на конденсаторе с течением времени, третий – производная от напряжения . Строим графики зависимости функций напряжения на конденсаторе и тока в цепи второго порядка при гармоническом воздействии E(t) (Приложение А).

Выполнение опытной части представляет собой проведение ряда опытов при изменении варьируемого параметра  и пронаблюдать изменение графика функции.

Изменяя варьируемый параметр , берем несколько значений больше собственной частоты колебательного контура и несколько меньше (Приложение Б).

Решаем несколько однотипных дифференциальных уравнений вида:

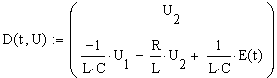
Находим максимальные значения амплитуды напряжения U(t):

Стоим графики зависимости функций напряжения на конденсаторе и тока в цепи второго порядка при гармоническом воздействии E(t) (Приложение Б).

Конечный шаг данной курсовой работы - построение графика амплитудо-частотной характеристики (Приложение Б)

При помощью математического пакета MatLab проверяем результаты проведённой работы и сравниваем их (Приложение В).

3.3 Выводы по результатам исследований

В проделанной работе мы с использованием системы MathCAD рассчитали значения функций напряжения на конденсаторе и тока в цепи второго порядка при гармоническом воздействии E(t). В результате,  получили графики функций напряжения на конденсаторе и тока в цепи.

Анализируя полученные графики, я сделал вывод: с увеличением частоты до частоты резонанса, наблюдается рост амплитуды тока и напряжения. При частоте резонанса, амплитуда тока и напряжения - максимальна. При дальнейшем увеличение частоты, наблюдается уменьшение амплитуды тока и напряжения. Численные данные приведены в таблице 3.

Таблица 3 - Численные данные зависимости амплитуды напряжения от частоты

          Построив график амплитудо-частотной характеристики можно заметить, что график имеет максимальное значение, т.е. экстремум, при резонансном значении частоты гармонического напряжения (Приложение Б).

Заключение

В данной курсовой работе был произведён анализ электрических процессов в цепях второго порядка  с использованием системы компьютерной математики MathCAD. Так же была произведена проверка в системе MatLab. После проделанной работы можно с уверенностью сказать, что семейство MathCAD успешно справляется с поставленными перед ним задачами, делая это намного быстрее, нежели сам человек. Данная система достаточно проста в освоении и может рекомендоваться в качестве главного помощника инженерам. Компьютерное моделирование с помощью этого пакета намного уменьшает время, усилия, затраченные на расчеты. Однако моделирование при помощи пакета MatLab сокращает время, усилия