



ЗАДАНИЕ № 1
Решение нелинейных алгебраических уравнений и их систем
При численном решении нелинейных алгебраических уравнений f(x)=0 возникают две задачи:
·
задача отделения корней, т.е. отыскания достаточно малых областей ![]() , в каждой из которых содержится
один и только один корень уравнения;
, в каждой из которых содержится
один и только один корень уравнения;
· задача определения значения корня с заданной степенью точности, если известно его начальное приближение в этой области.
Решение первой задачи выходит за рамки вычислительной математики и поэтому будем заниматься только решением второй, предполагая, что уже известна область D, внутри которой содержится единственный корень уравнения.
Для нахождения корня строится итерационная процедура
![]() , (1)
, (1)
причем функция ![]() конструируется так,
чтобы корень уравнения
конструируется так,
чтобы корень уравнения ![]() был одновременно и
корнем уравнения
был одновременно и
корнем уравнения ![]() . Если при этом в
некоторой окрестности корня выполняется неравенство
. Если при этом в
некоторой окрестности корня выполняется неравенство ![]() ,
то отображение (1) является сжатым и при выборе начального значения
,
то отображение (1) является сжатым и при выборе начального значения ![]() из этой окрестности
итерационный процесс (1) сходится к значению корня. Следует заметить, что это
условие является лишь достаточным, гарантирующим сходимость итераций (1), но не
является необходимым. Поэтому может оказаться так, что
из этой окрестности
итерационный процесс (1) сходится к значению корня. Следует заметить, что это
условие является лишь достаточным, гарантирующим сходимость итераций (1), но не
является необходимым. Поэтому может оказаться так, что ![]() выбран вне области сходимости,
а следующее приближение корня попадает в область сходимости и тогда итерационный
процесс сойдется.
выбран вне области сходимости,
а следующее приближение корня попадает в область сходимости и тогда итерационный
процесс сойдется.
Основной характеристикой численных методов решения нелинейных алгебраических уравнений является порядок скорости сходимости метода к корню уравнения. Метод имеет k-тый порядок скорости сходимости, если
![]() ,
,
где ![]() значение корня, C –
константа, не зависящая от номера итерации,
значение корня, C –
константа, не зависящая от номера итерации, ![]() -
два последовательных приближения к корню. Данная оценка справедлива только для
случая достаточно малого расстояния до корня, когда
-
два последовательных приближения к корню. Данная оценка справедлива только для
случая достаточно малого расстояния до корня, когда ![]() .
.
1. Метод дихотомии (метод деления отрезка пополам)
Пусть ![]() - непрерывная
функция, значение которой на концах интервала [a,b],
содержащего единственный корень уравнения, имеет разные знаки, т.е.
- непрерывная
функция, значение которой на концах интервала [a,b],
содержащего единственный корень уравнения, имеет разные знаки, т.е. ![]() . Тогда корень уравнения
находится с помощью следующего алгоритма:
. Тогда корень уравнения
находится с помощью следующего алгоритма:
1.
Полагаем ![]() .
.
2.
Вычисляем ![]() .
.
3.
Вычисляем ![]() и произведение
и произведение ![]() .
.
4.
Если ![]() , то
, то ![]() заменяем
на
заменяем
на ![]() и повторяем п.2, в противном
случае заменяем
и повторяем п.2, в противном
случае заменяем ![]() на
на ![]() и повторяем п.2.
и повторяем п.2.
Вычисления заканчиваются, когда ![]() ,
где
,
где ![]() - заданная точность. В качестве
значения корня принимается
- заданная точность. В качестве
значения корня принимается ![]() .
.
Метод имеет первый порядок скорости сходимости, поскольку на каждой итерации
![]() .
.
2. Метод Ньютона (метод касательных)
Пусть ![]() и корень уравнения
и корень уравнения ![]() является простым, т.е. в его
окрестности первая и вторая производные
является простым, т.е. в его
окрестности первая и вторая производные ![]() и
и
![]() знакопостоянные. Тогда
итерационный метод Ньютона запишется:
знакопостоянные. Тогда
итерационный метод Ньютона запишется:
![]() (2)
(2)
Для этого метода ![]() и начальная
точка
и начальная
точка ![]() должна выбираться из области
сходимости метода, т.е. из области, где
должна выбираться из области
сходимости метода, т.е. из области, где ![]() .
При указанных предположениях в достаточно малой окрестности корня метод имеет
второй порядок скорости сходимости.
.
При указанных предположениях в достаточно малой окрестности корня метод имеет
второй порядок скорости сходимости.
![]() , где
, где ![]() .
.
3. Методы Чебышева
Если функция обладает достаточной гладкостью и для нее существует обратная
функция, то для нахождения корня уравнения ![]() на
основе подхода, предложенного Чебышевым, можно построить методы произвольного
порядка по скорости сходимости. Так, метод третьего порядка представляется
следующим образом (
на
основе подхода, предложенного Чебышевым, можно построить методы произвольного
порядка по скорости сходимости. Так, метод третьего порядка представляется
следующим образом (![]() ):
):
![]() (3)
(3)
Для метода (3) ![]() и начальная
точка
и начальная
точка ![]() так же, как и для метода
Ньютона, должна выбираться из области, где
так же, как и для метода
Ньютона, должна выбираться из области, где ![]() .
Оценка скорости сходимости метода (3)
.
Оценка скорости сходимости метода (3)
![]() где
где ![]() -
функция, обратная по отношению к f(x).
-
функция, обратная по отношению к f(x).
4. Решение систем нелинейных уравнений
Для решения системы из n нелинейных алгебраических уравнений для n неизвестных
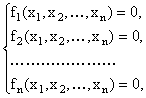 (4)
(4)
обычно используется метод Ньютона (2), который легко обобщается на случай системы уравнений (4)
![]()
![]() (5)
(5)
где
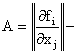 матрица Якоби,
матрица Якоби, ![]() ,
,![]() ,
,
![]() .
.
Условия сходимости метода (5) определяются теоремой Л.В.Канторовича,
которые, к сожалению, мало пригодны для практических вычислений. Поэтому обычно
приходится выбирать начальное значение вектора ![]() эмпирическим
путем.
эмпирическим
путем.
Задание
1. Напишите программу на Scilab, с помощью которой можно решить задачу отделения корней уравнений
![]() ;
;
![]()
путем построения их графиков на интервале ![]() . Подходящие границы интервалов
определите эмпирически.
. Подходящие границы интервалов
определите эмпирически.
2.
Напишите программу для
вычисления корней указанных уравнений всеми тремя методами (1) – (3) сразу при
заданном числе итераций (не более пятнадцати – двадцати итераций) с целью
сравнения скорости сходимости данных методов. Числовые значения приближенных
значений корней ![]() в зависимости от
номера итерации выводите на экран в виде таблицы, первый столбец которой есть
номер очередной итерации. Кроме этого, постройте графики зависимостей
в зависимости от
номера итерации выводите на экран в виде таблицы, первый столбец которой есть
номер очередной итерации. Кроме этого, постройте графики зависимостей ![]() для всех этих методов.
для всех этих методов.
3.
Объясните, почему для функции
![]() методы Ньютона и Чебышева не
сходятся, если начальное значение
методы Ньютона и Чебышева не
сходятся, если начальное значение ![]() . Найдите для
метода Ньютона значение
. Найдите для
метода Ньютона значение ![]() , при котором
этот метод гарантированно сходится.
, при котором
этот метод гарантированно сходится.
4.
Найдите кратный корень
уравнения ![]() методами (1) – (3). Объясните
замедление скорости сходимости методов (2) и (3) для этого примера.
методами (1) – (3). Объясните
замедление скорости сходимости методов (2) и (3) для этого примера.
5.
Для уравнения ![]() решите задачу отделения корней
и на основе анализа поведения функции
решите задачу отделения корней
и на основе анализа поведения функции ![]() в окрестности каждого корня определите области
сходимости для метода Ньютона. Для целей такого анализа постройте график
поведения этой функции в окрестности корней данного уравнения. Убедитесь, что
выбор начального приближения корня
в окрестности каждого корня определите области
сходимости для метода Ньютона. Для целей такого анализа постройте график
поведения этой функции в окрестности корней данного уравнения. Убедитесь, что
выбор начального приближения корня ![]() из области сходимости, где
из области сходимости, где ![]() , действительно гарантированно обеспечивает
сходимость метода и убедитесь в его расходимости в противном случае.
, действительно гарантированно обеспечивает
сходимость метода и убедитесь в его расходимости в противном случае.
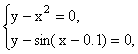
методом Ньютона (5), полагая ![]() . Убедитесь в том, что в
зависимости от выбора начального приближения, решение системы
сходится к различным корням.
. Убедитесь в том, что в
зависимости от выбора начального приближения, решение системы
сходится к различным корням.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.