Математика \ Численные методы

Правило увеличения точности приближенного решения

Страницы работы

2 страницы (Word-файл)
Скачать файл

Содержание работы

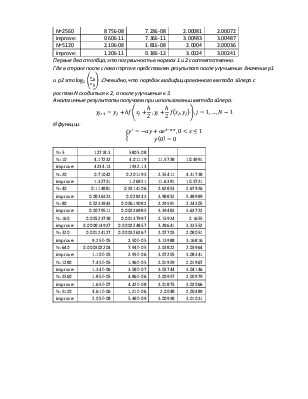
Для выбранного метода Эйлера примените правило увеличения точности приближенного решения  и экспериментально докажите, что порядок точности метода действительно повышается на один порядок  по h.

Возьмем модифицированный метод следующего вида:

И улучшим полученное решение с помощью правила:

Решим с помощью такого метода следующую задачу:

Погрешность решений была оценена с помощью локальной нормы (нормы 1):

И среднеквадратичной нормы (нормы 2):

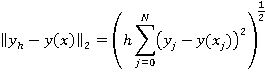
Получаем результат:

N

Eps1

Eps2

p1

p2

N=5

0.00650581

0.00386232

N=10

0.00663028

0.00555982

-0.0273407

-0.525572

improve:

0.044226

0.0379441

N=20

0.00154337

0.00127181

2.10299

2.12816

improve:

0.000316168

0.000244465

7.12806

7.2781

N=40

0.000371863

0.000306074

2.05324

2.05493

improve:

3.12E-05

2.40E-05

3.34235

3.34615

N=80

9.12E-05

7.52E-05

2.02765

2.0252

improve:

3.50E-06

2.68E-06

3.15673

3.164

N=160

2.26E-05

1.86E-05

2.01311

2.01206

improve:

4.13E-07

3.17E-07

3.0803

3.0799

N=320

5.62E-06

4.64E-06

2.00653

2.00589

improve:

5.03E-08

3.86E-08

3.03815

3.03943

N=640

1.40E-06

1.16E-06

2.00326

2.00291

improve:

6.21E-09

4.76E-09

3.01922

3.01958

N=1280

3.50E-07

2.89E-07

2.00162

2.00145

improve:

7.71E-10

5.91E-10

3.00965

3.00976

N=2560

8.75E-08

7.23E-08

2.00081

2.00072

improve:

9.60E-11

7.36E-11

3.00483

3.00487

N=5120

2.19E-08

1.81E-08

2.0004

2.00036

improve:

1.20E-11

9.18E-12

3.0024

3.00241

Первые два столбца, это погрешность в нормах 1 и 2 соответственно.

Где в строке после слова improve представлен результат после улучшения. Значения p1 и p2 это 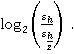Очевидно, что порядок модифицированного метода эйлера с ростом N сходиться к 2, а после улучшения к 3.

Аналогичные результаты получаем при использовании метода эйлера:

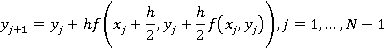
И функции:

N=5

12718.3

5805.08

N=10

4.17232

4.01119

11.5738

10.4991

improve:

4234.13

1932.13

N=20

0.71042

0.201193

2.55411

4.31738

improve:

1.32751

1.26921

11.6391

10.5721

N=40

0.114881

0.0314106

2.62853

2.67926

improve:

0.0836323

0.028243

3.98852

5.48989

N=80

0.0233943

0.00619082

2.29591

2.34305

improve:

0.0079511

0.00226985

3.39483

3.63722

N=160

0.00523738

0.00137997

2.15924

2.1655

improve:

0.000814927

0.000224857

3.28641

3.33552

N=320

0.00124127

0.000326267

2.07703

2.08051

improve:

9.25E-05

2.50E-05

3.13988

3.16816

N=640

0.000302204

7.94E-05

2.03822

2.03964

improve:

1.10E-05

2.95E-06

3.07205

3.08341

N=1280

7.45E-05

1.96E-05

2.01929

2.01967

improve:

1.34E-06

3.58E-07

3.03744

3.04146

N=2560

1.85E-05

4.86E-06

2.00957

2.00979

improve:

1.65E-07

4.42E-08

3.01875

3.02066

N=5120

4.61E-06

1.21E-06

2.0048

2.00489

improve:

2.05E-08

5.48E-09

3.00938

3.01031

Похожие материалы

Информация о работе

ВУЗ:
Новосибирский государственный университет (НГУ)
Предмет:
Численные методы
Тип:
Конспекты лекций
Категория:
Математика (Естествознание)
Размер файла:
20 Kb
Скачали:
0
Скачать файл