Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Имитационная модель формирования режима нагружения), страница 9

В теории вероятностей показывается, что по мере увеличение числа испытаний n₁ величина статистической вероятности P*(A) стремится по вероятности к теоретической вероятности P(A). Стремление по вероятности означает, что вероятность бесконечно малой разницы стремится к достоверному событию. Из сказанного следует, что в инженерных приложениях использовать вероятностные методы по их прямому назначению, т.е. для получения количественного абсолютного значения вероятностей, можно лишь применительно к массовым явлениям, повторяющимся многократно в сходных условиях.

Вероятность показателя надежности (вероятность разрушения) определяется интегрированием плотности вероятности q(R,F), когда сопротивление R меньше, чем сила F. Этот интеграл определяется

                                                            (6)

Если F и R независимы, это выражение преобразуется как

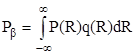,                                                          (7)

где P(R) вероятность превышения ледовой нагрузки и q(R) есть плотность вероятности сопротивления. Период времени T обычно принимается как срок службы сооружения.

Наиболее полным результатом вероятностного расчета является получение вероятностей для всех возможных значений, которые может принимать случайная величина. Такое сочетание вероятностей и возможных значений называют законом распределения случайной величины. С математической точки зрения закон распределения полностью определяет случайную величину. Он позволяет знать все свойства этой величины, а также прогнозировать эти свойства на будущее. говоря об особенностях вероятностных методов, необходимо коснуться еще одного важного вопроса - о соотношении этих методов и детерминистических. В инженерных приложениях эти методы тесно связаны и не только не исключают один другой, а дополняют друг друга. Ни одна инженерная задача не может быть решена вероятностными методами, если не начать ее рассмотрение с детерминистических позиций, и на долю вероятностных методов приходится лишь включение в эту задачу случайных факторов и специфических методов для их учета. Следовательно, решения вероятностных методов богаче по содержанию, а детерминистические дают только одно из возможных решений без оценки его вероятности.

Методы расчета надежности.

Для количественной оценки надежности применяются различные методы расчета надежности (см. Рис. 4): математические (формальные) методы и методы, учитывающие физические причины отказов.

При использовании математических методов расчета надежности принимают, что изменение надежности подчиняются некоторым статистическим закономерностям, которые определяются лишь экспериментально. При этом нельзя выяснить причины отказов и определить возможности их устранения, что является недостатком этих методов. Существует два направления этих методов: одно рассматривает надежность как временную категорию (надежность как качество, развернутое во времени), другое - как вероятность случайного события.

Математические методы первого направления применяют при расчете надежности конструкций, работоспособность которых лимитируется изнашиваемостью частей.

Математические методы расчета надежности изложены в работах таких видных ученых, как А.И. Берг, Н.Г. Бруевич, Б.В. Гнеденко.

Другое направление математических методов расчета надежности применимо к пироустройствам и устройствам, срабатывающим мгновенно и однократно. В этом случае по существу невозможно применить временные характеристики надежности, и надежность определяется из эксперимента как вероятность реализации случайного события.

Существует также два вида методов, учитывающих физические причины отказов: одно из них рассматривает надежность как вероятностную прочность, оперируя случайными величинами, другое - как вероятность невыброса случайного процесса (поля) за заданный уровень.