где Ф(g) - интеграл Лапласа.
Hаряду с надежностью, определяемой для всего установленного срока эксплуатации Т*, целесообразно рассматривать надежность P(t), достаточную к данному моменту времени t (0 <t<T*). Поскольку внешние воздействия на систему действуют в течение всего времени эксплуатации, а качество системы по мере эксплуатации ухудшается, то надежность P(t) обычно является убывающей функцией времени t.
Изменение надежности во времени может быть охарактеризовано частотой отказов, равной производной от функции надежности P(t) взятой с обратным знаком:
![]() (3)
(3)
Произведение P(t) dt представляет собой вероятность отказа в течение интервала времени (t, t+td). Другой характеристикой является интенсивность отказов:
![]() (4)
(4)
Произведение l(t)dt представляет собой условную вероятность отказа в течение интервала времени (t, t+dt) для системы, безотказно проработавшей время t. Hадежность выражается интенсивностью отказов следующим образом:
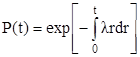 (5)
(5)
Если интенсивность отказов - l постоянна во времени, то из формулы (5) вытекает экспоненциальный закон распределения отказов l(t)
![]() (6)
(6)
Экспоненциальный закон широко применяется при расчете надежности радиотехнических и электронных устройств.
Понятие надежности тесно связано с понятием долговечности. За время долговечности обычно принимается либо время работы системы, либо полная наработка (т.е. суммарное время полезного функционирования).
Долговечность системы Т является случайной величиной. Распределение этой величины может быть выражено через функцию надежности.
Пусть, например, эксплуатация системы прекращается после первого отказа. Тогда функция распределения долговечности F(T) определяется по формуле:
![]() ,
(7)
,
(7)
где t=T.Здесь P(t) - функция надежности системы. Плотность распределения долговечности P(T) совпадает при этом с частотой отказов P(t), при t=T средняя долговечность вычисляется по формуле:
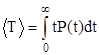 (8)
(8)
Отсюда после интегрирования по частям и использование формулы (3) получаем:
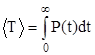 (9)
(9)
Из приведенных соображений видно, что между понятиями надежности и долговечности имеются состояния взаимности.
Очевидна необходимость рассмотрения процесса изменения функции надежности во времени на протяжении всего установленного срока службы.
Для экспоненциального закона распределения (6) формула (9) дает:
![]() (10)
(10)
Таким образом, интенсивность отказов при экспоненциальном законе надежности равна обратной величине от математического ожидания долговечности. Формула (6) принимает вид:
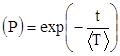 (11)
(11)
При рассмотрении отказов серьезного характера, означающих полный выход системы из строя, когда восстановление или ремонт становятся нецелесообразными, когда отказы создают опасность для людей и окружающей среды и т.п., вместо понятия интенсивности отказов используется эквивалентное, но психологически более приемлемое понятие риска в единицах времени. Если срок службы измеряется годами, то говорят о годовом риске.
Величину риска в единицах времени обозначают через g.Поскольку со временем элементы конструкции утрачивают часть совей несущей способности из-за накопления усталостных повреждений и пластических деформаций, из-за коррозии и т.п., то годовой риск, вообще говоря, - возрастающая функция времени t. Hаряду с переменным риском r(t) можно ввести также риск, осредненный на некотором отрезке времени, например, [0,t]. Очевидно, что осредненный риск:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.