Теоретические основы методов оценки показателей надежности

3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДОВ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ

3.1. Метод расчета показателей надежности при использовании марковских процессов

Слайд 75/197

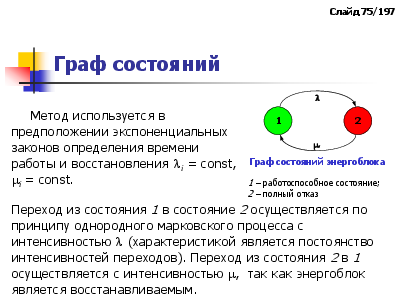
Граф состояний



Метод используется в предположении экспоненциальных законов определения времени работы и восстановления i = const, i = const.

1

2



Граф состояний энергоблока 1 – работоспособное состояние; 2 – полный отказ

Переход из состояния 1 в состояние 2 осуществляется по принципу однородного марковского процесса с интенсивностью  (характеристикой является постоянство интенсивностей переходов). Переход из состояния 2 в 1 осуществляется с интенсивностью , так как энергоблок является восстанавливаемым.

Слайд 76/197

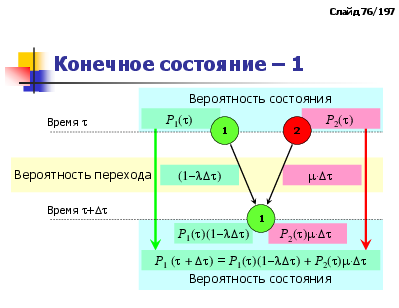
Конечное состояние – 1

Вероятность состояния

Р1()

Р2()

Время 

1

2

Вероятность перехода

(1)



Время +

1

Вероятность состояния

Р1()(1)

Р2()

Р1 ( + ) = Р1()(1) + Р2()

Слайд 77/197

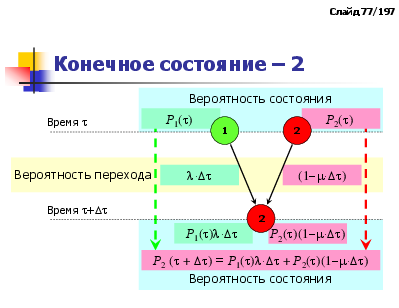
Конечное состояние – 2

Вероятность состояния

Р1()

Р2()

Время 

1

2

Вероятность перехода



(1)

Время +

2

Вероятность состояния

Р1()

Р2()(1)

Р2 ( + ) = Р1() + Р2()(1)

Слайд 78/197

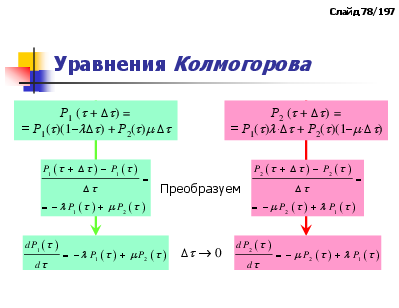
Уравнения Колмогорова

Р1 ( + ) = = Р1()(1) + Р2()

Р2 ( + ) = = Р1() + Р2()(1)

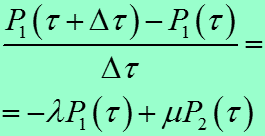
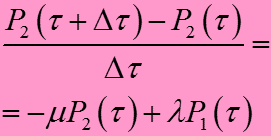
Преобразуем

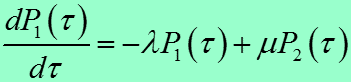
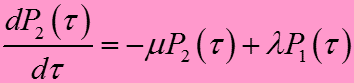
  0

Слайд 79/197

Правило составления уравнений Колмогорова

Производная вероятности (нахождения элемента в каждом из состояний) по времени равна алгебраической сумме произведений вероятностей состояний (связанных между собой стрелками на графе) на интенсивность переходов, при этом слагаемые берутся со знаком минус, если стрелка выходит из вершины, для которой записывается уравнение, и со знаком плюс, если стрелка входит в вершину графа.

Слайд 80/197

Решение уравнений Колмогорова

Для решения системы уравнений Колмогорова дополнительно вводится уравнение нормировки

Применительно к исследуемому графу можно записать (опуская для простоты записи ):

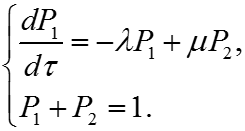
Слайд 81/197

Стационарный режим

При    устанавливается стационарный режим, для которого система уравнений запишется как

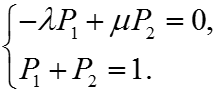
Из решения следует, что

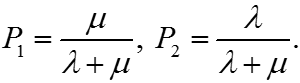
Слайд 82/197

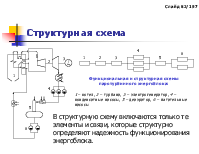
Структурная схема

4

6

1

2

3

5

3

2

1

Функциональная и структурная схемы паротурбинного энергоблока: 1 – котел, 2 – турбина, 3 – электрогенератор, 4 – конденсатные насосы, 5 – деаэратор, 6 – питательные насосы

4

5

В структурную схему включаются только те элементы и связи, которые структурно определяют надежность функционирования энергоблока.

6

Слайд 83/197

Группы элементов

По влиянию на надежность элементы функциональной тепловой схемы энергоблока можно разделить на четыре группы:

• элементы, отказ которых приводит к полному останову энергоблока;
• элементы, отказ которых приводит к уменьшению энергетической производительности;
• элементы, отказ которых приводит к понижению экономичности энергоблока;
• элементы системы управления и аварийной защиты.

Слайд 84/197

Граф состояний

На основе структурной схемы разделяются состояния энергоблока на работоспособные и неработоспособные, строится граф состояний. Граф включает только достижимые состояния. Число возможных состояний:

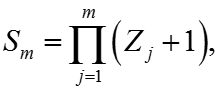
где m – количество элементов структурной схемы, Z – количество однотипных единиц оборудования, составляющих данный сложный элемент

Слайд 85/197

Достижимые состояния

Число достижимых состояний находится как

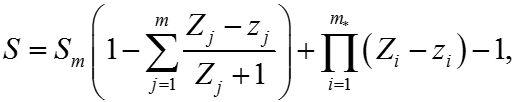
где m – число сложных элементов в схеме, для которых Zj > zj – максимального количества отказавших единиц оборудования, при котором наступает отказ сложного элемента и как следствие – энергоблока.

Слайд 86/197

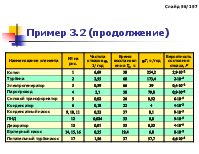
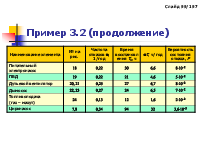
Пример 3.1

котел

турбогенератор

1

2

Определить коэффициент готовности энергоблока, состоящего из котла и турбогенератора, структурная схема которого приведена на рисунке. Интенсивности отказов элементов: 1 = 210-4 ч-1; 2 = 110-4 ч-1. Интенсивности восстановлений: 1 = 110-2 ч-1; 2 = 1,2510-2 ч-1.

1

0

1

1

2

2

2

3

Структурная схема энергоблока и граф достижимых состояний

Слайд 87/197

Пример 3.1 (продолжение)

Структурная схема состоит из двух элементов, m = 2. Число возможных состояний

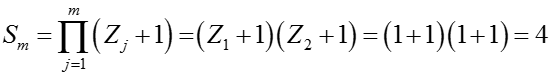
так как Z1 = 1, Z2 = 1.

Число достижимых состояний

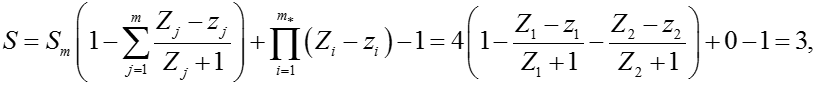
так как Z1 = z1, Z2 = z2, m = 0 (отсутствуют сложные элементы, для которых Zj > zj).

Достижимые состояния: (0) = (0, 0) – энергоблок работоспособен; (1) = (1, 0) – энергоблок неработоспособен; (2) = (0, 1) – энергоблок неработоспособен. Состояние (3) = (1, 1) – недостижимо

Слайд 88/197

Пример 3.1 (продолжение)

Система уравнений Колмогорова:

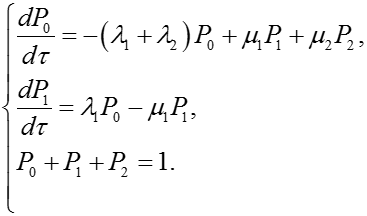
Решая систему, например, методом преобразований Лапласа, найдем вероятность работоспособного состояния Р0, которая совпадает с нестационарным значением коэффициента готовности КГ()

Слайд 89/197

Пример 3.1 (продолжение)

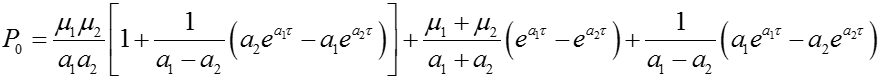
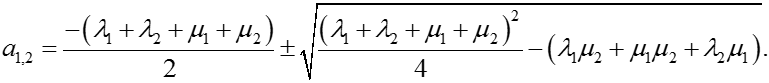
где

Подставляя значения 1, 2, 1, 2, найдем а1 = -1,02110-2; а2 = -1,25810-2. Из выражения для Р0 следует, что при  = 0 Р0 = 1, а при   

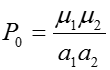
Слайд 90/197

Пример 3.1 (продолжение)

Результаты расчета по полученной формуле приведены на рисунке. Из рисунка следует, что при  > 400 ч КГ() приближается к стационарному