Расчет сопла Лаваля. Определение термодинамических параметров и скорости воздуха на входе в минимальное сечение и на выходе из сопла

Министерство Образования Республики Беларусь

Белорусский Национальный Технический Университет

Кафедра' Теплогазоснабжение и вентиляция'

Расчетно-графическая работа

'Расчет Сопла Лаваля'

Выполнил:

                                                                                           студент группы

                                                                        Проверила:

Минск 2002.

Теория вопроса.

Для увеличения скорости потока применяют специальные каналы, называемые соплами.

Сопло представляет собой канал, суживающийся в направлении движения потока.

Рассмотрим процесс обратимого, т.е. без трения, адиабатного истечения газа из сопла, соединенного с газовым  резервом большого объема. Параметры газа в резервуаре обозначим через P_1,V₁,T₁, а давление на выходе из сопла P₂. Будем считать, что давление газа на выходе из сопла равно давлению среды, в которую поступает газ. Скорость газа на входе в сопло-ω_1.

Определяем скорость истечения газа из сопла ω₂ по известным значениям ω₁, P_1,V₁,T₁.

Эта задача может быть решена по уравнению:

                                                               (1)

при этом для определения перепада энтальпий удобно воспользоваться h,S-диаграммой.

Можно решить эту задачу и другим способом:

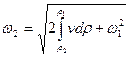                                                                      (2)

где    вычисляется по экспериментальным данным по p,v зависимости.

Задача определения ω₂ с помощью уравнения (2) легко решается для случая испытания идеального газа.

Из уравнения адиабаты получаем:                                           (3) 

Подставляя это значение в уравнение (2) и интегрируя получаем для скорости истечения газа из сопла:

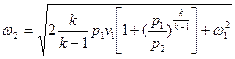                                                             (4)

Если скорость потока на входе в сопло ω₁ пренебрежительно мала по сравнению с ω₂, то уравнение (4) записывается:

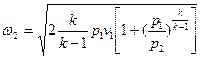                                                                     (5)

Как видно из этого уравнения, скорость истечения газа из сопла ω тем больше, чем меньше величина отношения давлений p₁/p_2.

    Период давлений p₂/p₁=β при котором скорость истечения равна скорости звука, скорость истечения и сечение сопла, в котором образуется такая скорость, называются критическими и обозначаются соответственно: β_кр, ω_кр, t_кр.

Критическая скорость истечения (скорость в критическом сечении сопла) определяется выражением:

                                                                (6)                                                                                                (7)

Путем сопоставления формул (5) и (7) можно получить значение критического перепада давления , т.е. перепада, при котором устанавливается критическая скорость истечения:

                                                                                           (8)

Расход газа через сопло М вычисляется следующим образом. Объем газа, вытекающего из сопла в единицу времени, v, равен:

v=v₂M                                                     (9)

где v₂- удельный объем газа в выходном сечении сопла.

С другой стороны, v=fω                                                                            (10)

где f- площадь выходного сечения сопла.

Отсюда следует число                                                                    (11)

Заменяя в этом уравнении v₂ с помощью уравнения адиабаты , получаем:

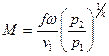                                                                                               (12)

Подставляя сюда значение ω из уравнения (5) имеем:

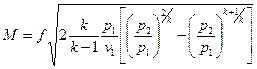                                                             (13)

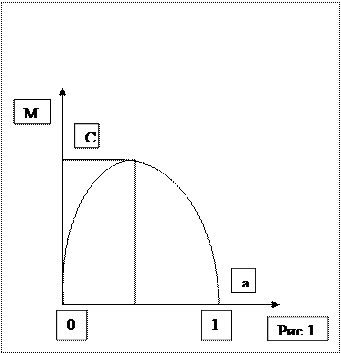
На рисунке 1 в соответствии с уравнением (13)  представлена зависимость расхода газа через суживающиеся сопло от перепада давления. Приведенная зависимость свидетельствует о том, что расход газа увеличивается при изменении перепада давления β от единицы до β_кр  (участок a-b) и затем остается неизменным, равным критическому расходу М_кр.

(участок b-c); участок, определяемый формулой (13) он не имеет физического смысла.

Постоянный расход при β<β_кр объясняется тем, что в выходном сечении суживающегося сопла устанавливается критическая скорость.

Значение критического расхода можно получить путем подстановки β_кр (8) в формулу (13), в результате чего имеем:

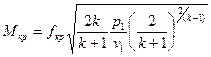                                                                  (14)

при истечении идеального газа через суживающее сопло из емкости неограниченных объемов расчет скорости истечения и расхода следует вести по формулам (5) и (13) при условии, что β>β_кр и по формулам (7) и (14) при β≤β_кр.