Механика жидкости и газа: Курс лекций (Основы теории подобия и размерностей. Истечение вязкой жидкости из отверстий и насадок)

входе в него струя жидкости испытывает сжатие точно так же, как при истечении из отверстия, но поскольку она ограничена боковой стенкой насадка, то внутри него образуется кольцевая вихревая область (в сечении с). Ввиду того, что скорость в сжатом сечении больше, чем в выходном (это следует из условия неразрывности, или постоянства расхода), давление в сжатом сечении становится меньше атмосферного в силу уравнения Бернулли, примененного для этих двух сечений. Таким образом, в сжатом сечении насадка возникает вакуум, и, следовательно, течение жидкости на участке от свободной поверхности жидкости в резервуаре до сжатого сечения в насадке происходит под большим напором, нежели в случае его отсутствия. Поэтому скорость в сжатом сечении насадка будет больше, чем в сжатом сечении струи, вытекающей из отверстия при одинаковом напоре H. А это значит, что расход через насадок будет больше, чем через отверстие, при одинаковой их выходной площади. Следует, однако, отметить, что в случае использования насадка появляются дополнительные потери, обусловленные расширением потока после сжатого сечения и потери на трение о стенки насадка. Как показывают расчетные и экспериментальные данные, при длине насадка  эти потери меньше, чем выигрыш в действующем напоре. Поэтому данный насадок увеличивает расход жидкости, а еще большего эффекта можно достичь, используя конический расходящийся насадок с безотрывным режимом течения в диффузоре. Расчетные формулы для насадков имеют тот же вид, как для отверстия, однако, величина коэффициентов в них будет определяться конкретным типом насадка и зависеть не только от числа Рейнольдса, но также от относительной длины насадка .

В случае истечения из резервуара с переменным уровнем жидкости, вообще говоря, для расчетов следует использовать уравнение Бернулли в нестационарной форме. Однако, если процессы опорожнения или наполнения резервуара происходят достаточно медленно и ускорения жидкости малы, то можно применить уравнение Бернулли для установившегося течения, рассматривая течение как последовательную смену стационарных состояний, для каждого из которых применимы уравнения установившегося движения.

Рассмотрим процесс наполнения (опорожнения) резервуара, при котором часть жидкости вытекает через отверстие или насадок, но имеет место также приток жидкости в резервуар с постоянным расходом Q_п, не равным, вообще говоря, расходу истечения Q₀.

Чтобы связать время изменения уровня жидкости в резервуаре с расходами, составим уравнение баланса объемов жидкости для слоя жидкости, расположенного на уровне z от выходного сечения отверстия (см. рисунок). Если за время dt уровень жидкости изменился на dz, то, очевидно, что: , где Ω – площадь поперечного сечения. Отсюда

 и время изменения уровня от Н₁ до Н₂ может быть определено интегрированием:

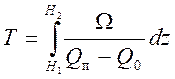
Полагая для простоты форму резервуара цилиндрической и заменяя расход истечения по выведенной ранее формуле ( уровень жидкости Н = z):

,

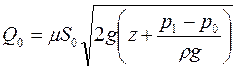а принимая, что избыточное давление отсутствует, т.е. р₁ = p₀  получим:

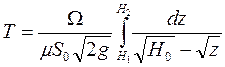 , где Н₁ и Н₂ – начальное и конечное положение уровней жидкости в процессе ее течения, а Т – время, за которое это произошло. В вышеприведенной формуле введено обозначение напора Н₀, как уровня, при котором приток жидкости равен расходу истечения: Q_п = Q₀ =

Если теперь вычислить интеграл, то получим:

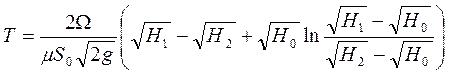
Из данного соотношения, очевидно, что если , то , что означает установление стационарного режима, когда приток равен расходу и устанавливается режим течения с постоянным уровнем в резервуаре.

Если же Н₀ = 0, т.е. приток отсутствует, то время опорожнения резервуара определится более просто:

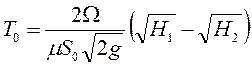, а в случае наличия над свободной поверхностью избыточного давления p_м = p₁ – p₀, соответственно, по формуле:

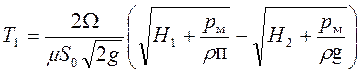
Наибольший вакуум, возникающий внутри цилиндрического насадка в сжатом сечении струи можно вычислить, используя уравнение Бернулли для выходного и сжатого сечений струи:

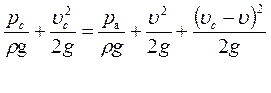, где последний член определяет потери напора при резком расширении потока от сжатого сечения до выходного, вычисленные в соответствии с формулой Борда. Преобразуя это выражение, можно получить:

.

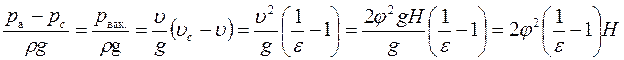Здесь использовано также условие постоянства расхода .

Из полученной формулы следует важный для практики вывод: истечение через цилиндрический насадок в атмосферу с заполнением выходного сечения возможно только при напорах, меньших предельного Н_пр., который соответствует снижению давления в сжатом сечении до давления насыщенных паров жидкости при данных условиях, т.е р_с =р_н.п.:

.

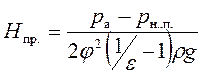При Н > Н_пр. происходит срыв режима работы насадка: струя жидкости отрывается от стенок и процесс истечения осуществляется как из отверстия с острой кромкой.

В случае истечения через насадок затопленной струи жидкости при некотором предельном напоре, конкретная величина которого определяется давлением насыщенных паров жидкости и заглублением насадка, будет наблюдаться кавитационный режим течения, сопровождающийся образованием и схлопыванием газовых пузырьков.

6 ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДНЫХ СИСТЕМ

Трубопроводы, используемые в различных технических устройствах обычно подразделяются на две группы: а.) - простые, не содержащие ответвлений и представляющие собой одну или несколько последовательно соединенных труб, вообще говоря, разной длины и диаметров; б.) - сложные, образованные путем разветвлений, боковых отводов, замыканий