умножаем числитель и знаменатель
написанной дроби на комплексное число ![]() , сопряженное знаменателю. Заранее должны оговориться, что на нуль делить нельзя, и что, поэтому, знаменатель
, сопряженное знаменателю. Заранее должны оговориться, что на нуль делить нельзя, и что, поэтому, знаменатель ![]() не
равен нулю.
не
равен нулю.
![]()
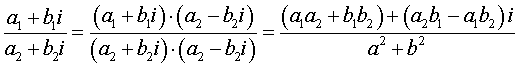 ,
,
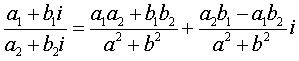 (9)
(9)
Формула (9) показывает, что отношение двух комплексных чисел есть комплексное число, если только знаменатель дроби не есть нуль. Деление же на нуль невозможно так же, как и в случае действительных чисел.
Общее заключение из формул (4), (5), (6) и (9): все четыре действия арифметики, проделанные над комплексными числами, дают в результате опять комплексное число, могущее оказаться, в частном случае, и действительным.
Из того, что, во время выкладок, позволено
обращаться с мнимой единицей i как с действительным переменным, заменяя только всюду, по дороге и в окончательном результате, ![]() через
-1, следует, что все законы арифметики и алгебры распространяются полностью на
комплексные числа. В частности, произведение комплексных
чисел
через
-1, следует, что все законы арифметики и алгебры распространяются полностью на
комплексные числа. В частности, произведение комплексных
чисел ![]() обра
щается в
нуль тогда и только тогда, когда один из множителей является нулем.
обра
щается в
нуль тогда и только тогда, когда один из множителей является нулем.
2. Геометрическое изображение комплексных величин.
Мы знаем, что всякое действительное число а изобразимо
в виде точки М, лежащей на прямой линии и, что, обратно, всякая такая точка М изображает некоторое действительное число а, называемое абсциссою точки М . Абсцисса точки М есть отвлеченное действительное число, выражающее длину направленного отрезка ОМ, измеренного единицей масштаба.
Аналогично, всякое комплексное число
![]() изобразимо
в виде точки М (а, Ь) плоскости, имеющей абсциссою и
ординатою действительные числа а и
Ь, и обратно: всякая точка М плоскости, имеющая
абсциссою
изобразимо
в виде точки М (а, Ь) плоскости, имеющей абсциссою и
ординатою действительные числа а и
Ь, и обратно: всякая точка М плоскости, имеющая
абсциссою
действительное число а,
и ординатою действительное число b, служит изображением комплексного числа ![]()
По аналогии с предыдущим, это комплексное
число![]() называется
называется
аффиксом точки М. Таким образом, всякое комплексное число ![]() есть
аффикс единственной вполне определенной точки М,
лежащей на плоскости ХОУ, и всякая точка М(а, b) этой-плоскости имеет своим аффиксом
комплексное число
есть
аффикс единственной вполне определенной точки М,
лежащей на плоскости ХОУ, и всякая точка М(а, b) этой-плоскости имеет своим аффиксом
комплексное число![]() .
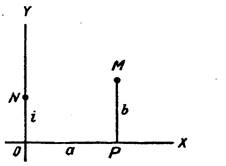
Если
точка М лежит на горизонтальной координатной оси ОХ,
то аффикс такой точки М есть действительное число а,потому что в этом случае b = 0. Поэтому ось
абсцисс ОХ носит название оси
действительных чисел или сокращенно: действительная ось. Аналогично,
когда точка М лежит на вертикальной координатной оси ОУ, аффикс такой точки М есть
чисто мнимое число bi,
потому что в этом случае а=0. Поэтому
ось ординат О У носит название оси
мнимых чисел или сокращенно (но неправильно): мнимая ось. Точка N оси ординат ОУ, находящаяся
выше начала О и отстоящая от него
.
Если
точка М лежит на горизонтальной координатной оси ОХ,
то аффикс такой точки М есть действительное число а,потому что в этом случае b = 0. Поэтому ось
абсцисс ОХ носит название оси
действительных чисел или сокращенно: действительная ось. Аналогично,
когда точка М лежит на вертикальной координатной оси ОУ, аффикс такой точки М есть
чисто мнимое число bi,
потому что в этом случае а=0. Поэтому
ось ординат О У носит название оси
мнимых чисел или сокращенно (но неправильно): мнимая ось. Точка N оси ординат ОУ, находящаяся
выше начала О и отстоящая от него
на единицу масштаба 1, имеет своим аффиксом мнимую единицу i. Аффикс начала О есть нуль.
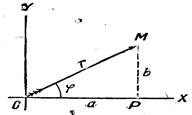
Если мы соединим точку М с началом О прямолинейным отрезком, то
получим вектор ОМ, направленный из начала О в рассматриваемую
точку М.
Этот вектор ОМ также
хорошо может служить для геометрического изображения комплексного числа ![]() , как и его конец М.
, как и его конец М.
Для комплексного числа ![]() вектор ОМ направлен по плоскости.
Его длину мы обозначим через r,
а его наклон к положительной части оси ОХ обозначим
через
вектор ОМ направлен по плоскости.
Его длину мы обозначим через r,
а его наклон к положительной части оси ОХ обозначим
через ![]() .
Из прямоугольного треугольника ОРМ мы имеем известные прямыеформулы преобразования прямоугольника координат а, b в полярные r,
.
Из прямоугольного треугольника ОРМ мы имеем известные прямыеформулы преобразования прямоугольника координат а, b в полярные r,![]()
![]() (10)
(10)
и обратные формулы
перехода от полярных координат r,![]() к прямоугольным а, b
к прямоугольным а, b
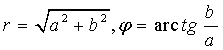 (11)
(11)
Так как функция ![]() есть
многозначная, то надо условиться в оценке угла
есть
многозначная, то надо условиться в оценке угла ![]() .
Угол
.
Угол ![]() отсчитывается
всегда в положительном направлении (против стрелки часов), т. е. вращением
положительной части оси ОХ до положения вектора ОМ. Если этот угол
отсчитывается
всегда в положительном направлении (против стрелки часов), т. е. вращением
положительной части оси ОХ до положения вектора ОМ. Если этот угол ![]() , то остальные значения будут:
, то остальные значения будут: ![]() и
т. д., когда вектор ОМ проходится многократным
непрерывным вращением
и
т. д., когда вектор ОМ проходится многократным
непрерывным вращением
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.