Проектирование цифрового фильтра (тип фильтра – ФВЧ, границы полосы пропускания – 3600 Гц, границы полосы непропускания – 1800 Гц)

Функция передачи фильтра Баттерворта не имеет нулей, а её полюсы расположены в левой полу-плоскости комплексной переменной S.

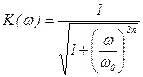, где  n – порядок фильтра Баттерворта;

ω – частота среза.

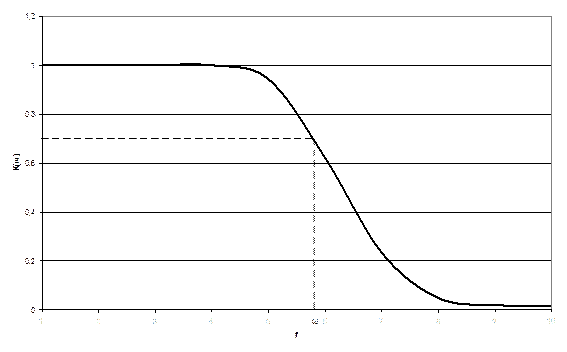
Рисунок 1 - АЧХ фильтра Баттерворта

На f=0, K(ω)=1. На f=ω,  дБ для любого порядка фильтра. Чем выше порядок фильтра тем более прямоугольный характер носит АЧХ.

Воспользуемся методом билинейного преобразования. Данный метод позволяет синтезировать цифровой фильтр по частотным характеристикам аналогового фильтра-прототипа.

Между аналоговыми и цифровыми частотами существует зависимость, связанная с tg:

.

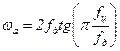Тогда расчет даст следующие значения:

;

.

При помощи программы MicroCAP получены следующие значения:

;

.

Теперь нужно перейти из S-области в Z-область. Согласно методу бинарного преобразования данный переход можно осуществить при помощи следующей формулы:

;

.

Получится:

.

.

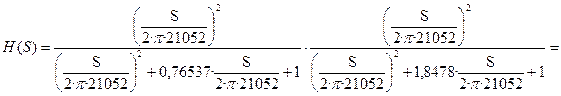
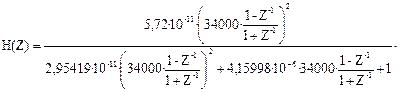
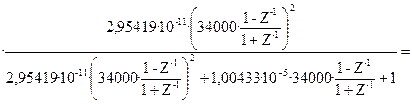
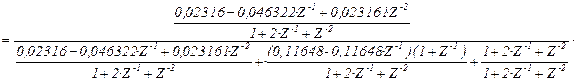
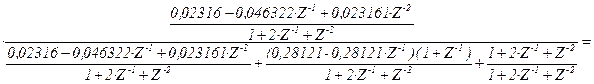
получена следующая передаточная функция фильтра-прототипа:

Проверка на устойчивость

При анализе работы любой цифровой структуры важное место приобретает вопрос устойчивости. Если по каким-либо причинам цепь оказывается неустойчивой, то вместо желаемого фильтра получают генератор.

Для того чтобы фильтр был устойчивым, полюсы его передаточной функции   должны располагаться внутри единичного круга плоскости Z.

Для определения устойчивости цепи, необходимо найти полюса передаточной функции, то есть корни знаменателя.

1.

D=b²-4ac

D=1,71429² - 4·1·0,79559=-0,244

   

Данная функция имеет корни Z_1/2=-0,857±j0,247

2.

D=b²-4ac

D=1,49779² - 4·1·0,56882=-0,032

    

Данная функция имеет корни Z_3/4=-0,749±j0,089

Полюсы передаточной функции лежат в плоскости единичной окружности на плоскости Z, следовательно цепь устойчивая.

Импульсная характеристика

Для того чтобы найти импульсную характеристику, для начала нужно преобразовать передаточную функцию, получаем:

.

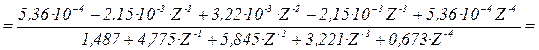
Получена импульсная характеристика данного фильтра:

1	-4 z-1	+6 z-2	-4 z-3	+1 z-4	1+3,212 z-1+3,932 z-2+2,167 z-3+0,453 z-4
1	+3,2 z-1	+3,9 z-2	+2,2 z-3	+0,5 z-4	1-7,212 z-1+25,234 z-2-58,863 z-3+106,025 z-4-160,520 z-5+214,829 z-6-261,966 z-7
	-7,2 z-1	+2,1 z-2	-6,2 z-3	+0,5 z-4
	-7,2 z-1	-23,2 z-2	-28,4 z-3	-15,6 z-4	-3,3 z-5
		25,2 z-2	+22,2 z-3	+16,2 z-4	+3,3 z-5
		25,2 z-2	+81,1 z-3	+99,2 z-4	+54,7 z-5	+11,4 z-6
			-58,9 z-3	-83,0 z-4	-51,4 z-5	-11,4 z-6
			-58,9 z-3	-189,1 z-4	-231,5 z-5	-127,5 z-6	-26,6 z-7
				106,0 z-4	+180,0 z-5	+116,1 z-6	+26,6 z-7
				106,0 z-4	+340,6 z-5	+416,9 z-6	229,7 z-7	+48,0 z-8
					-160,5 z-5	-300,8 z-6	-203,1 z-7	-48,0 z-8
					-160,5 z-5	-515,6 z-6	-631,2 z-7	-347,8 z-8	-72,6 z-9
						214,8 z-6	+428,1 z-7	+299,8 z-8	+72,6 z-9
						214,8 z-6	+690,0 z-7	+844,7 z-8	+465,5 z-9	+97,2 z-10
							-262,0 z-7	-544,9 z-8	-392,8 z-9	-97,2 z-10
							-262,0 z-7	-841,5 z-8	-1030,1 z-9	-567,6 z-10	-118,6 z-11
								296,6 z-8	+637,2 z-9	+470,4 z-10	+118,6 z-11

Расчет спектра входного воздействия и комплексной передаточной характеристики фильтра с помощью быстрого преобразования Фурье (БПФ)

Быстрое преобразование Фурье (БПФ) устанавливает связь между отсчетами во временной и частотной областях. Формула БПФ для входного сигнала:

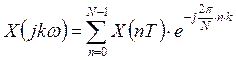
где: N – количество отсчетов во временной и частотной областях;                    - весовая функция.

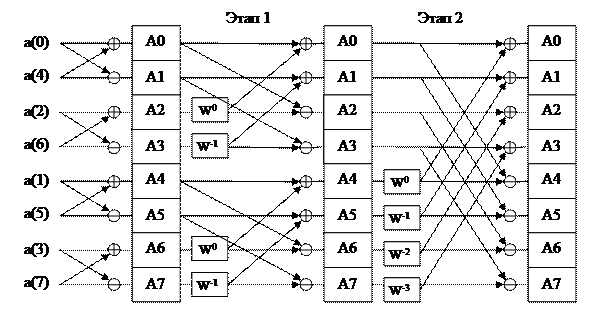
Рисунок 2 - Алгоритм БПФ

Так как количество отсчетов N=8, БПФ производится в два этапа. Определяем для каждого из этапов значения весовых функций.

Этап 1.      Количество взаимодействующих элементов – 4,

;  ;

Этап 2.      Количество взаимодействующих элементов – 8,

;  ;

; 

Исходные отсчеты подаются на вход не в естественном порядке. На рисунке 2   изображена так называемая «бабочка». Это графический алгоритм быстрого преобразования Фурье. Состоит из простых элементов: сумматоров, вычитателей и есть так же элементы домножения на весовые функции. Числа на вход подаются в определенной последовательности, на выходе получаются комплексные числа .

При расчете  исходной последовательностью является импульсная характеристика , которая определяется по передаточной характеристике .

Заданная последовательность:

Произведен расчет спектра входного сигнала и данные приведены в рисунке 3.

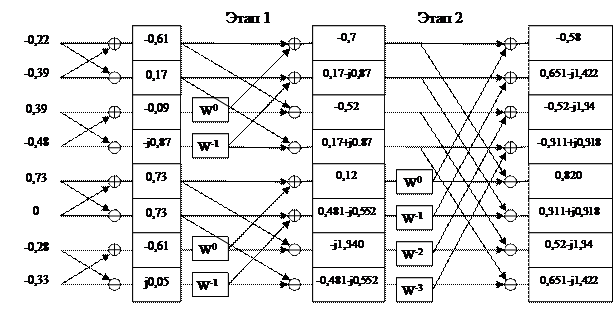
Рисунок 3 – Алгоритм БПФ с результатами вычислений  X(jkω)

Быстрое преобразование Фурье позволило путем простейших расчетов, получить следующие значения входного сигнала :

Теперь рассчитаем :

Значения:

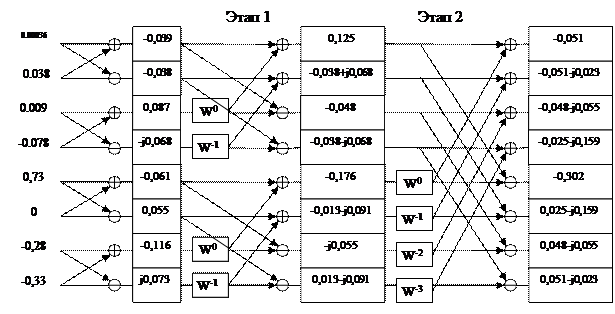
Рисунок 4 – Алгоритм БПФ с результатами вычислений  H(jkω)

Расчет свертки во временной и частотной областях входного воздействия и заданной передаточной характеристики. С помощью ОБПФ расчет выходного воздействия

Произведем расчет свертки заданных последовательностей во временной области:

Будем использовать круговую свертку перекрытие суммированием