Разработка корреляционного фильтра. Разработка функциональной схемы

2.Описание корреляционного фильтра

Пусть S1=A*cos w1*t и S2=cos w2*t. Время длительности сигналов равно T, априорные вероятности передачи P(S1) и P(S2), помехи флюктационные, функция плотности распределения которых имеет гауссовский закон распределения

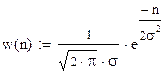 где - дисперсия помех.

Задан критерия оптимального приема: идеальный наблюдатель, который минимизирует среднюю вероятность ошибки

                      Pош = P(S1)*P(y2/S1) + P(S2)*P(y1/S2)

Найдем оптимально правило решения и структурную схему оптимального приемника.

Для решения задачи используем общее для приемников двоичных сигналов правило принятия. 

                               ,

если , то принимается решение в пользу S1, иначе – S2.Для упрощения решения положим, что P(S1)=P(S2)=0.5; тогда 

 

    2. Для определения функций правдоподобия  и  предположим, что на вход приемника поступает сигнал x(t)=S1(t)+n(t)

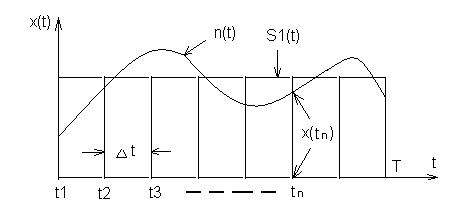рис. 1

Возьмем n отсчетов сигнала x(t) через одинаковые интервалы  , равные интервалу корреляции помехи . Рассмотрим отсчетные значения суммы сигнала S1(t) и n(t) в различных сечениях ti. Так как расстояние между сечениями равно интервалу корреляции, эти сечения некоррелированы между собой, а так кА помеха распределена по гауссовскому закону, то сечения также и независимы.

В 1-ом сечении x(t1)=S1(t1)+n(t1)

Во 2-ом сечении x(t2)=S1(t2)+n(t2)

В к-ом сечении x(tk)=S1(tk)+n(tk).

Плотность вероятности, благодаря независимости сечений, будет равна произведению одномерных плотностей вероятности различных сечений

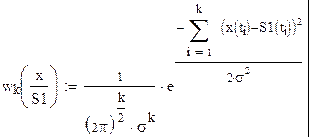
Тогда отношение правдоподобия

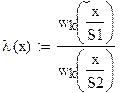, и согласно правилу решения, если вычисленное значение , то приемник должен выдать сигнал S1, в противном случае - сигнал S2. Отсюда получается оптимальное правило решения в виде неравенства

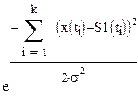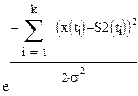   > , то S1.

Прологарифмируем это выражение

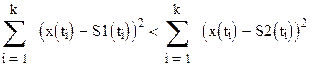, то S1.

Таким образом оптимальный приемник работает следующим образом: определяется среднеквадратическое отклонение поступившего не вход приемника сигнала x(t) от обоих ожидаемых сигналов и выносится решение в пользу того сигнала, где это среднеквадратическое отклонение меньше.

В интегральной форме получим

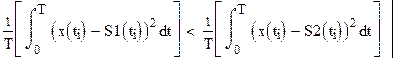, то S1, или более компактно .

Раскрыв скобки, получим , то S1, или

, то S1.

Т.е. если функция взаимной корреляции входного сигнала x(t) и S1(t) больше, чем функция взаимной корреляции входного сигнала x(t) и S2(t), то x(t) содержит, кроме помехи, сигнал S1(t).

Схема реализующая это правило решения называется корреляционным приемником(фильтром).

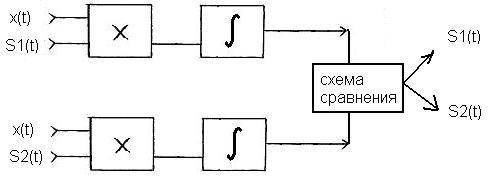
рис. 2

Цифровой коррелятор выполнен по схеме рис. 3 на цифровом перемножителе D1 и накапливающем сумматоре,  состоящем из сумматора D2 и элемента памяти - регистра D3.  

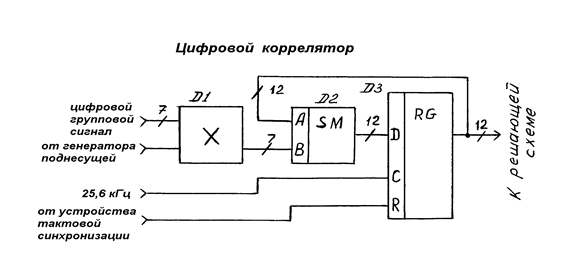
3.Разработка программы.

3.1 Расчет параметров.

Число периодов колебания сигнала с частотой поднесущей на одно сообщение (посылку) находится так:

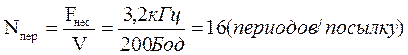
   Число отсчетов сигнала на одном периоде колебания определяется как:

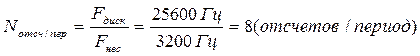
Так как всего в ПЗУ находится 256 отсчетов, то мы будем брать каждый 256/8=32-ой отсчет. 

Таким образом, количество отсчетов необходимое для передачи одного сообщения равно:

 

Сдвиг на 90⁰ соответствует 64-ому отсчету, на 270⁰ 192-ому отсчету в массиве синуса.

3.2. Обобщенный алгоритм работы фильтра