Разработка обобщенной структурной схемы системы связи для передачи непрерывных сообщений дискретными сигналами (амплитуда канальных сигналов – 12 мВ, максимальная частота аналогового сигнала – 7,2 кГц)

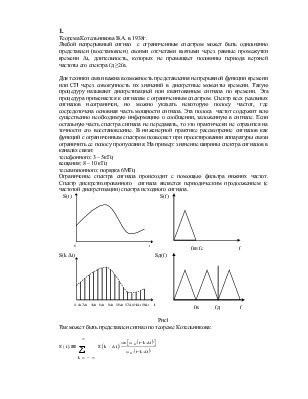
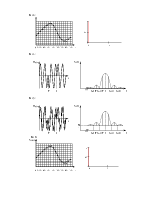
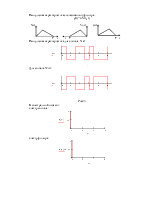
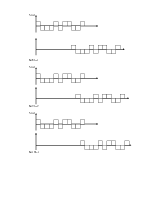
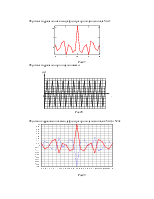
Если характеристика фильтра не идеальна, то спектральная плотность на выходе находится как:

Gвых(f)=G(f)K²(f)

Тогда дисперсия:

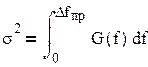
Предположим, что спектральная плотность помехи распределена равномерно:

N₀

Характеристика ФНЧ имеет вид:

                         К(f)

fc                           f

Следовательно, дисперсию можно найти как площадь прямоугольника с основанием Df_пр и высотой равной N₀:

σ² = Df_пр∙ N₀ = 36,36∙10³∙9,2∙10^-11 = 3,345∙10^-6 (Вт)

Среднеквадратическое отклонение будет равно σ = 1,828∙10^-3.

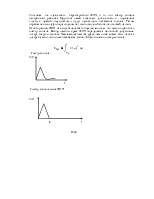
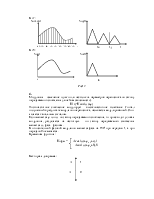
Плотность распределения флюктуационной помехи с нулевым математическим ожиданием распределена по нормальному закону:

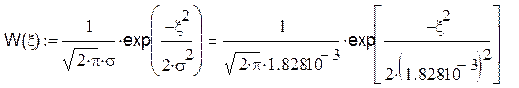
Кривая плотности распределения W(ξ):

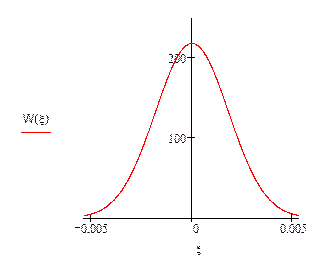
Рис17

Плотности распределения  с ненулевым математическим ожиданием будут распределены по закону Релея-Райса.

Плотность распределения W(z/0):

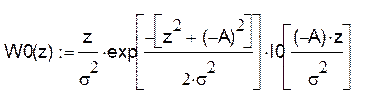
Плотность распределения W(z/1):

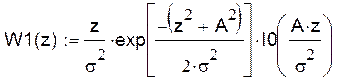
Так как в закон Релея-Райса входит функция Бесселя, которая неопределенна в отрицательной области, я сдвигаю кривые на математическое ожидание равное А.

Тогда получаю:

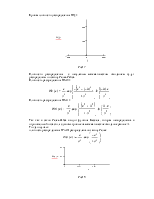
плотность распределения W(z/0) распределена по закону Релея:

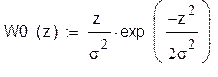
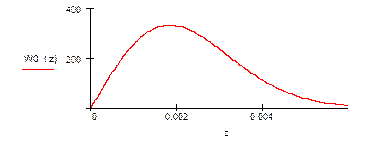
Рис18

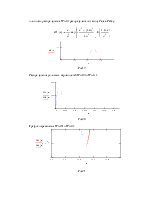
плотность распределения W(z/1) распределена по закону Релея-Райсу:

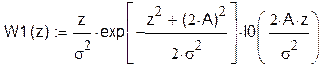
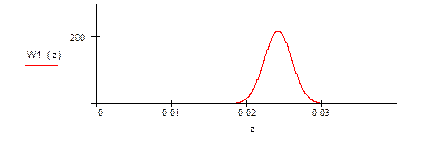
Рис19

Распределения условных вероятностей W(z/0) и W(z/1):

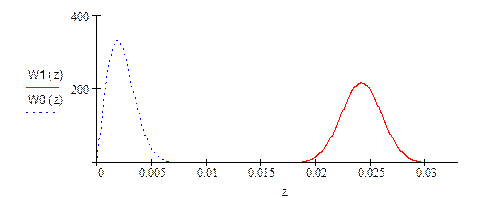
Рис20

График пересечения W(z/0) и W(z/1):

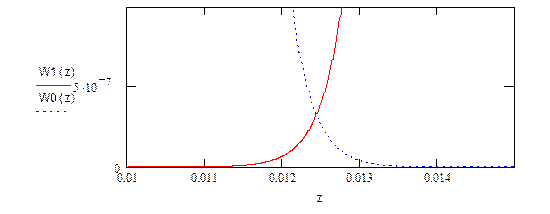
Рис21

Принятие решение по одному отсчету смеси сигнала и помехи  z(t₀)  = x_i (t₀ )+ x(t₀) на интервале элемента сигнала длительности Т:

- значение отсчета принятой смеси сигнала и помехи на входе  приемника.

Вычисляем отношение правдоподобия:

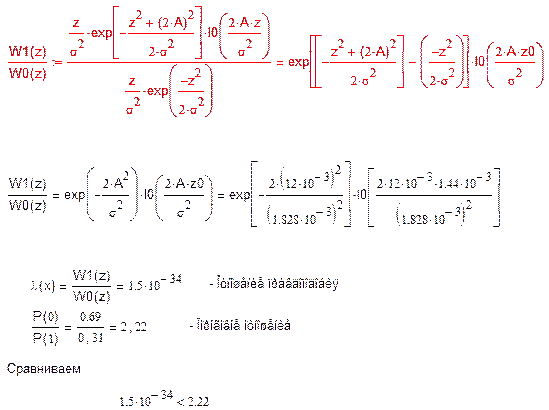
Приемник примет решение в пользу сигнала x2, т.е. примет 0.

6.

При приеме сигнала по одному отсчету, отношение сигнал/шум на выходе рассматриваемого приемника определяется следующим образом:

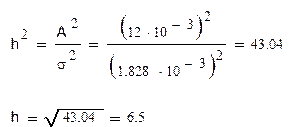
Вероятность ошибки в неоптимальном некогерентном приемнике ОФМ:

Кривая помехоустойчивости ОФМ:

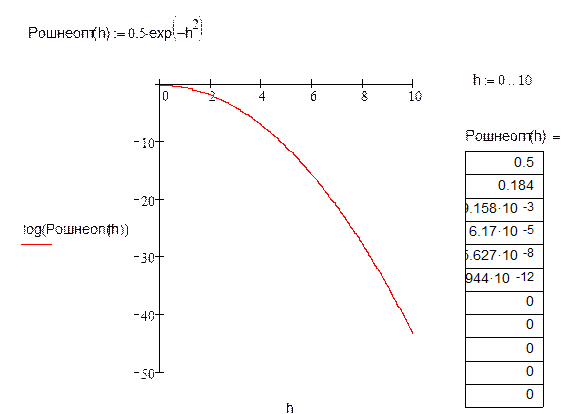
Рис22

7.

Оптимальный приемник – приемник, который обеспечивает максимум помехоустойчивости при заданных сигналах и заданной помехи. Потенциальная помехоустойчивость – от предел помехоустойчивости приема при заданном методе передачи и заданном уровне помехи. Оптимальный приемник наилучшим образом обрабатывает поступающий на его вход сигнал. Он обеспечивает большое отношение сигнал/шум и маленькую вероятность ошибки одновременно. Такой приемник называется приемником Котельникова. Приемник Котельникова называется еще когерентным, то есть нужно знать все параметры сигнала и когда он передавался.

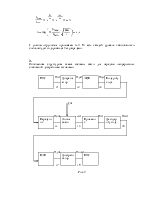
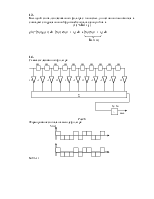
Существует две схемы приемника Котельникова:

T                                        T

1/T∫(z(t)-x1(t))²dt < 1/T∫(z(t)-x2(t))²dt  =>x1

0                                         0

T                                        T

 1/T∫(z(t)-x1(t))²dt  > 1/T∫(z(t)-x2(t))²dt  =>x2

0                                         0

В идеальном приемнике Котельникова решение принимается в пользу того сигнала, для которого минимально среднеквадратическое отклонение от смеси сигнала и шума приходящего на вход.

Схема приемника Котельникова:

                                       x1(t)

			( )2		1/T∫

1

x2(t)

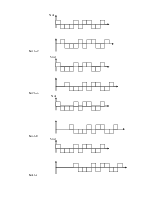
Другая схема:

Вычисление функции корреляции. Решение выносится в пользу того сигнала, у которого функция корреляции больше похожа на получивщуюся.

                                       x1(t)                                     Pсрx1/2

			1/T∫

                                                                                                                         1

x2(t)                                   Pсрx2/2

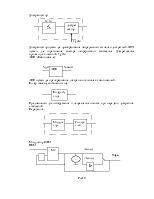
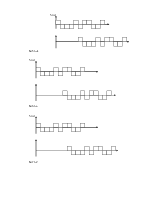
Приемник Котельникова для ОФМ:

                                          Ucosωt                                               1

a

                                                                                                       0

0

Рис23

Вероятность ошибки в таком приемнике для ОФМ равна:

Рошофм ≈ 2 Рошфм(1- Рошфм), где

Рошфм = ½[1-Ф(√2h)]

Приемник Котельникова является идеальной  моделью приемника, его параметры не достижимы. Это достигается благодаря тому, что при приеме учитываются все параметры сигнала. Решение о приеме сигнала осуществляется в конце каждого интервала, для чего в приемнике должна имеется специальная система синхронизации элементов сигнала.

Полоса пропускания оптимальный приемник 1/T и она равна эффективной полосе сигнала, а значит уровень помехи меньше на выходе приемника. Если полоса в 2 раза больше, как у неоптимального фильтра, уровень помехи на его выходе будет больше. Из-за этого отношение сигнал/шум при оптимального больше, то есть уровень полезного сигнал больше.

Максимально возможное отношение сигнал/шум определятся по следующей формуле:

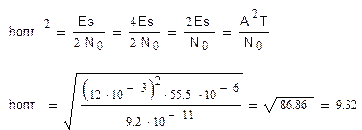
Выигрыш в отношении сигнал/шум оптимального приемника по сравнению с рассчитанным в пункте 6:

8.

Оптимальный приемник обеспечивает при заданных условиях минимум вероятности ошибки, поэтому его помехоустойчивость, как и помехоустойчивость системы связи в целом называется потенциальной (предельно достижимой).

Вероятность ошибки в оптимальном приемнике Котельникова:

9.

Методы накопления используются для точного определения приходящего сигнала.

Сущность: Одна и та же информация передается по n параллельным