Помехоустойчивость систем связи. Разработка обобщенной структурной схемы системы связи для передачи непрерывных сообщений дискретными сигналами (амплитуда канальных сигналов – 12 мВ)

Решение в данном случае принимается с использованием пороговой решающей схемы синхронным способом. При расчете считаем, что длительность сигнала возросла в k-раз по сравнению со случаями использования простых сигналов, где n – количество элементарных посылок в сложном сигнале.

p_ошАМкг = ,       

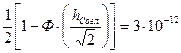При увеличении длительности сигнала уменьшается вероятность ошибок.

Синхронные способ лучше, т.к. ключ замыкается только в момент главного максимума графика выходного сигнала, и все значения побочных максимумов не повлияют на принятие решения.

20. Пропускная способность разработанной системы связи

Система связи служит для передачи сообщений от отправителя к получателю. Однако не всякое сообщение содержит информацию. Информация – это совокупность сведений об объекте или явлении, которые увеличивают знания потребителя об этом объекте или явлении.

В теории информации исходят из того, что в некотором сообщении x_iколичество информации I(x_i) зависит не от ее конкретного содержания, а от того, каким образом выбирается данное сообщение из общей совокупности возможных сообщений.

В реальных условиях выбор конкретного сообщения производится с априорной вероятностью p(x_i). Чем меньше эта вероятность, тем больше информации содержится в данном сообщении.

При определении количества информации исходят из следующих требований:

1.  Количественная мера информации должна обладать свойством аддитивности: количество информации в нескольких независимых сообщениях должно равняться сумме количества информации в каждом сообщении.

2.  Количество информации в достоверном событии должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном явлении.

Указанным требованиям удовлетворяет логарифмическая мера, определяемая формулой

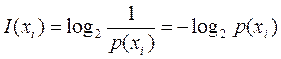
В теории информации чаще всего необходимо знать не количество информации, содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником сообщений.

Если имеется ансамбль из k сообщений x₁, x₂,…x_k с вероятностями p(x_i)…p(x_k), то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений H(x), определяется формулой

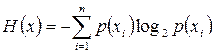, бит/сообщ.

, бит/сообщ.

Производительность источника определяется количеством информации, передаваемой в единицу времени. Производительность двоичного источника информации Н^¢(х) определяется формулой:

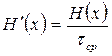                            , бит/с.

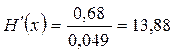, бит/с.

где t_ср=1/V - длительность элемента сообщения, а V - скорость передачи сообщений, Бод.

Увеличить производительность можно путем уменьшения длительности элементов сообщения, однако возможность эта ограничивается полосой пропускания канала связи. Поэтому производительность источника можно увеличить за счет более экономного использования полосы пропускания.

Пропускной способностью канала связи С называется максимально возможная скорость передачи информации по каналу.

Пропускная способность непрерывного канала связи определяется по формуле Шеннона

, бит/с,                                      

где  Df_пр - полоса пропускания канала связи, h² - отношение средней мощности сигнала к средней мощности помехи,  h² = Р_с /Р_н .

,бит/с

Наконец, пропускная способность дискретного (двоичного) канала связи со скоростью передачи V и вероятностью ошибки  p  равна

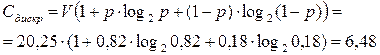, бит/с.

Эффективность системы связи можно оценить по величине отношения пропускной способности дискретного канала к производительности источника сообщений и по величине отношения пропускной способности дискретного канала связи  к пропускной способности непрерывного канала связи.

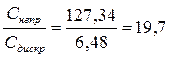
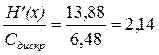
Так как производительность источника больше пропускной способности дискретного канала, то возможна передача информация по каналу связи.