Общие сведения о системах электросвязи. Детерминированные сигналы, их классификация. Разложение сигналов в ряд по ортогональным функциям, страница 8

1. Функция взаимной корреляции.
2. Характеризует связь между сечениями разных случайных процессов.

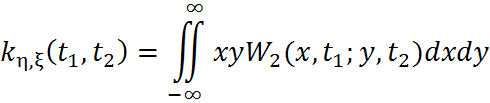
Замечание: Если два процесса независимы, то их функция взаимной корреляции равна нулю.

7.2 Стационарные случайные процессы.

Случайные процессы

Стационарные (установившиеся)

Нестационарные (неустановившиеся)

Стационарные в широком смысле

Стационарные в узком смысле

Стационарность в широком смысле – случайный процесс , у которого числовые характеристики не зависят от времени, а функция корреляции зависит от интервала между отсчётами.

Если процесс стационарен в узком смысле, то он стационарен и в широком смысле, а наоборот не всегда верно.

Свойства стационарности в узком смысле случайных процессов:

1. .
2. .
3. .
4. .
5. .

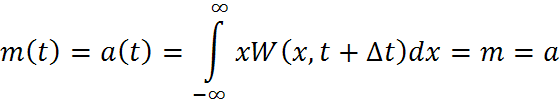
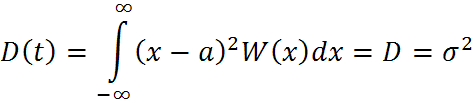
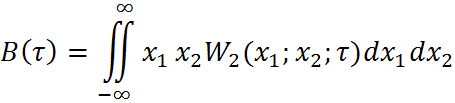
СП называется стационарным в широком смысле, если его числовые характеристики не зависят от времени(то есть выполняются условия 1, 2, 3, 4, 5).

Свойства функций корреляции в стационарных процессах:

1. Функция корреляции действительная и чётная, так как это функция времени.
2. .

Если

- Полная мощность процесса

При

- Мощность переменной составляющей

• Мощность постоянной
• составляющей

Интервал корреляции.

Интервал корреляции – это минимальное расстояние между двумя сечениями, при котором значения случайных величин можно считать некоррелированными.

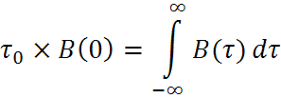
(1)

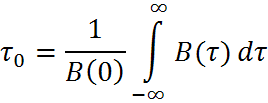
Формула (1) определяется как основание эквивалентного прямоугольника, площадь которого равна площади под кривой

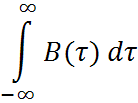
Нормированная функция корреляции.

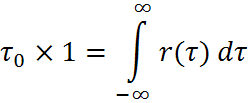
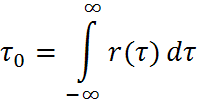
Практически

7.3 Теорема эргодичности.

Для эргодических случайных процессов статические характеристики можно определить не только усреднением по ослаблению (по множеству), но и усреднением по времени одной реализацией случайного процесса. При этом числовые характеристики, полученные по одной реализации путём усреднения по времени периода наблюдения . Теоретически . Вероятность близка к 1 и совпадает с соответствующей характеристикой, полученной путём усреднения по ослаблению(по множеству).

Усреднение по множеству:

Усреднение по времени:

Свойство эргодичности стационарных случайных процессов имеет большое практическое значение. Для таких процессов одна реализация полностью определяет характеристики или свойства случайного процесса в целом .

Усреднение по множеству

Усреднение по времени

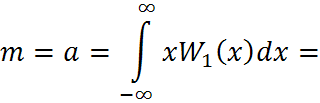
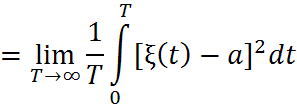
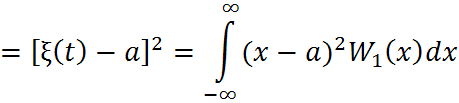
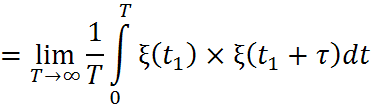
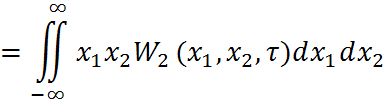
7.4 Гауссовский(нормальный) случайный процесс и его свойства.

Гауссовским называется такой процесс, у которого мгновенные значения распределены по нормальному закону:

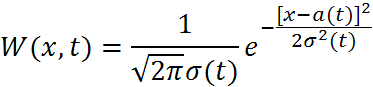
(1)

Если не менять

Интегральная функция распределения нормального процесса.

(2)

Произведя замену в формуле (2) получим:

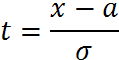
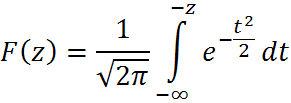
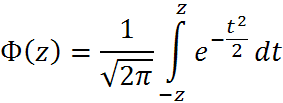
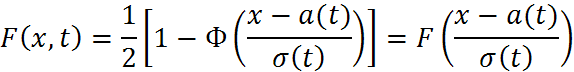
Свойства нормального процесса.

1. Стационарность в широком смысле эквивалентна стационарности в узком смысле.
2. Условие эргодичности: , то есть интеграл сходится.
3. Сечения независимы, если они некоррелированы.
4. Линейные преобразования не изменяют функции вероятности(вида кривой).
5. Сумма нормального случайного процесса и детерминированной функции не
6. изменяет закон распределения.

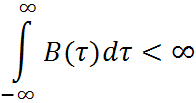
7.5 Функция корреляции одиночного прямоугольного импульса.

Случайные процессы могут быть периодические и непериодические.

Функция корреляции.

Напишем функцию корреляции отдельно:

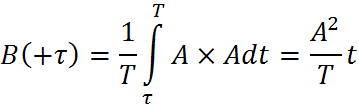
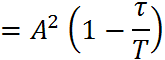
Функция корреляции непериодическая

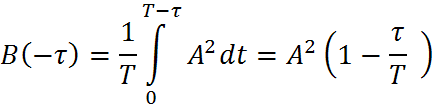
Окончательно:

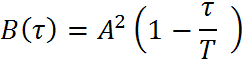
Функция корреляции чётная.

Функция корреляции периодического сигнала.

ДАМ

Учитывая тригонометрические преобразования, в результате получим:

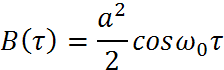
Функция корреляции также периодическая.

Функция корреляции будет иметь вид:

Вывод: У периодического сигнала функция корреляции является периодической функцией с той же частотой .

7.6 Применение корреляционных методов обработки сигналов в технике связи.

Устройства, позволяющие определить функцию корреляции называются корреляционными.

• Существует два способа приёма:
• Взаимнокорреляционный.
• Автокорреляционный.

Рассмотрим первый способ.

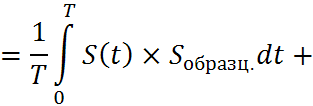
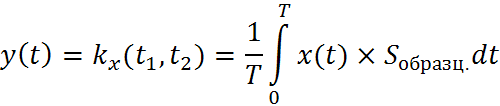
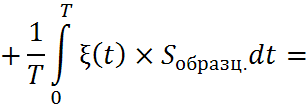
Рассмотрим второй способ.

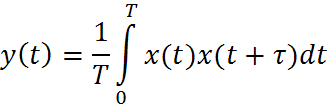
- функция автокорреляции сигнала.

- функции взаимной корреляции.

- функция автокорреляции помехи.

- мощность сигнала

Отсчет лучше делать в конце длительности сигнала.

Данный способ называется – выделение сигнала на фоне помех.