Общие сведения о системах электросвязи. Детерминированные сигналы, их классификация. Разложение сигналов в ряд по ортогональным функциям, страница 2

Это модулированные сигналы.

1.4 Разложение сигналов в ряд по ортогональным функциям.

Для исследования различных свойств сообщений (сигналов и помех) используются их разложения в ортогональные ряды (функции).

Любой сигнал или помеху можно представить в виде ряда:

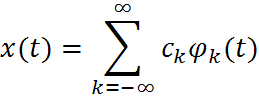
- Ортогональные простейшие функции, неслучайные. Например:

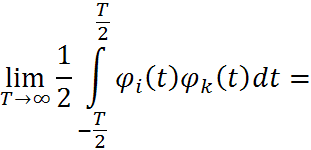
, если

, если

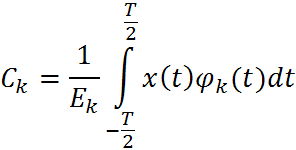
- Случайный коэффициент:

- Энергия ортогональных функций.

Доказательство теоремы Котельникова основывается на преобразовании Фурье.

;

;

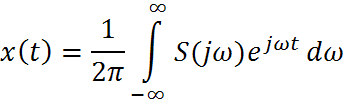
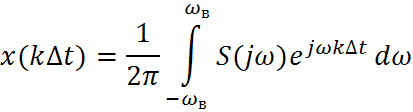
С математической точки зрения теорема Котельникова означает представление сигнала в виде ряда:

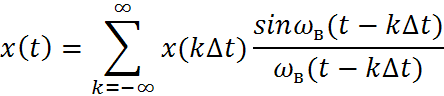
(1)

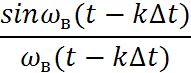
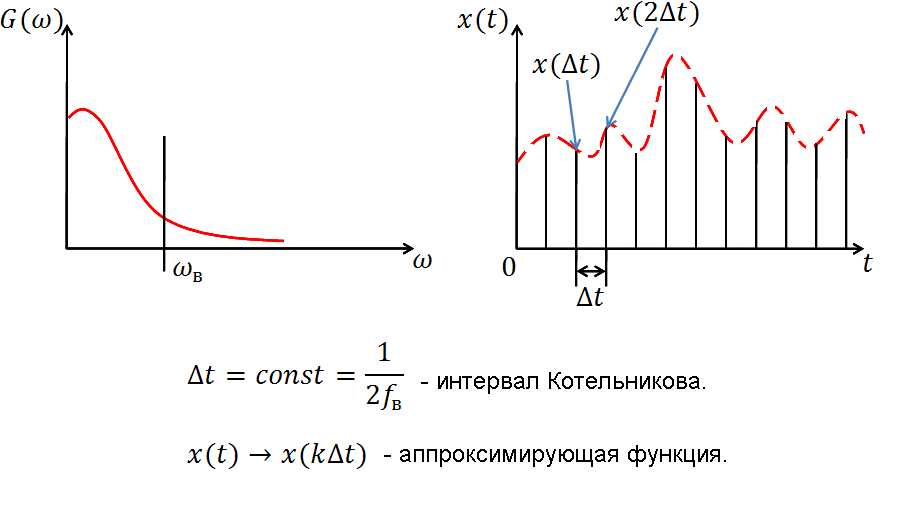
Где в формуле (1) - отсчёты, ( ), - функция отсчётов, - наивысшая частота спектра сигнала.

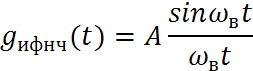
2. Нельзя получить ИФНЧ.

Рассмотрим простейший ФНЧ (RC - цепочка).

Реальный.

Исходный (идеальный).

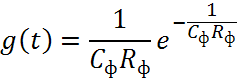
Импульсная характеристика нашего ФНЧ:

Вывод: Чем выше и чем ближе характеристика ФНЧ приближается к идеальной, тем точнее восстановление переданного сигнала.

1. Линейные электрические цепи (ЛЭЦ).

Для ЛЭЦ справедлив принцип суперпозиции: реакция на суммарное воздействие равна сумме реакций на каждое из воздействий в отдельности.

Пример:

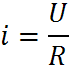
- Характеристика цепи.

Пусть

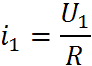
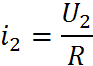
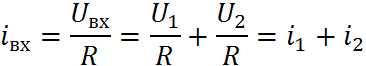
Тогда , а

В ЛЭЦ невозможно появление новых частот, не содержащихся во входных сигналах.

2. Нелинейные электрические цепи (НЭЦ).

Для НЭЦ неприменим принцип суперпозиции.

Пример:

;

;

В НЭЦ возникают новые частоты, не содержащихся во входных воздействиях, это положительный момент.

3. Параметрические электрические цепи (ПЭЦ).

• Для ПЭЦ:
• Справедлив принцип суперпозиции.
• Возникают новые частоты, не содержащиеся во входных воздействиях.

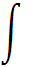
ПЭЦ конструируются на основе НЭ, на которые подаются напряжения, зависимые от времени.

Пример:

ПЭЦ

2.2 Принципы преобразования сигналов.

На входе

На выходе

Спектр воздействия:

Функция плотности вероятностей:

Функция распределения вероятностей:

Математическое ожидание:

Дисперсия:

Функция корреляции:

Интервал корреляции:

Коэффициент корреляции:

Энергетический спектр:

Полоса спектра:

• Преобразования бывают:
• Пассивные – преобразование, при котором не возникает новых частот.
• 2. Активные – преобразование, при котором появление новых частот имеет
• большое значение в технике связи. Активное преобразование предполагает
• использование либо нелинейных элементов, либо параметрических элементов.
• При использовании нелинейных элементов мы используем аппроксимации НЭ:
• Степенной полином. Метод тригонометрических функций.
• Отрезками прямых линий. Метод угла отсечки.

Пример степенного полинома:

- Характеристика НЭЦ

- Возмущение воздействия

Тогда получим:

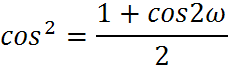
Так как

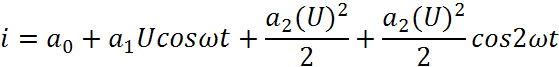
Амплитуда 1-й гармоники

Постоянная составляющая

Амплитуда 2-й гармоники

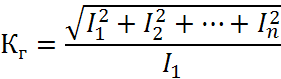
Бигармоническое колебание для нелинейного элемента:

Если

, и

Тогда,

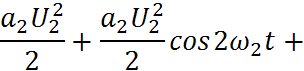
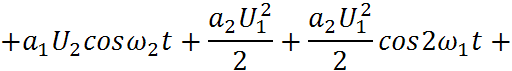
Кратные гармоники появляются за счёт квадратичного члена, а суммарно-разностные в результате умножения частот (перекрестные члены).

Бигармоническое колебание для параметрического элемента:

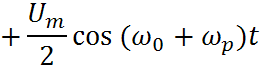
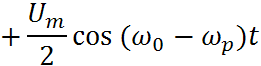
При преобразованиях, кроме НЭ, часто используются фильтры, то есть линейные элементы.

2.3 Виды преобразований спектров сигналов.

1. Умножение частоты, то есть умножение частоты в целое число раз.

АЧХ фильтра

2. Деление частоты. (в целое число раз).

3. Преобразование частоты, то есть получение суммарно - разностных частот.

Самый простой преобразователь:

Д

АЧХ

Модулированные колебания меньше искажаются в канале связи, чем Н.Ч. сигналы, так как Н.Ч. относительно широкополосные, а Модулированные – узкополосные.

• Вывод:
• Преобразования используются для борьбы с искажениями.
• При преобразованиях можно использовать частотную селекцию, которая
• используется в многоканальных системах связи.

4. Модуляция.