АИМ в чистом виде не используется в силу низкой помехоустойчивости, но лежит в основе получения ИКМ.
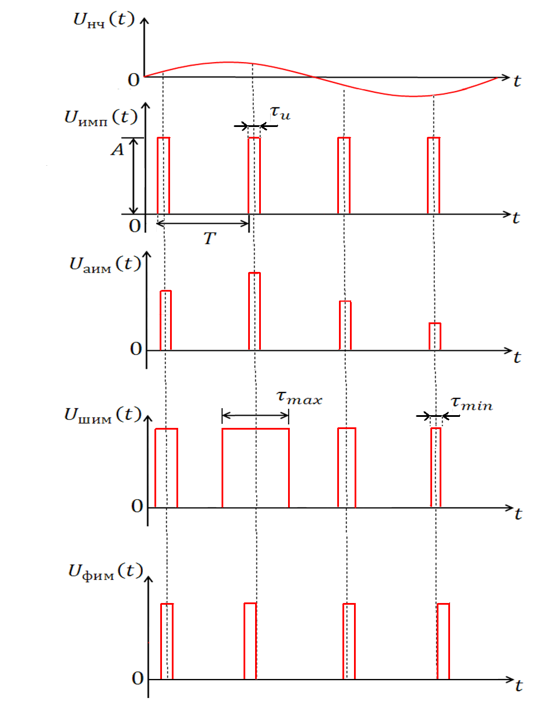
Спектр Амплитудно-Импульсной Модуляции.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6.1 Импульсно-кодовая модуляция (ИКМ).
ИКМ – один из возможных методов импульсной модуляции, который суммирует в себе все положительные свойства дискретизации, квантования и кодирования.
Сущность ИКМ. Непрерывное сообщение дискретизируется по времени по теореме Котельникова, полученные отсчёты квантуются, то есть дискретизируются по амплитуде, полученная последовательность квантованных значений непрерывного сообщения кодируется в виде последовательностей кодовых комбинаций. Кодирование сводится к записи номера уровня в двоичной системе счисления. Передача отдельных значений сигнала сводится к передаче определённых групп импульсов. Эти группы импульсов передаются друг за другом через относительно большие промежутки времени по сравнению с длительностью отдельных импульсов.
ИКМ - код
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Динамический диапазон квантованных сигналов.
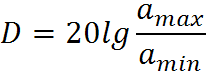
Количество уровней.
![]()
Интервал квантования.
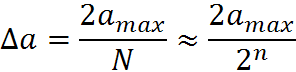
Мощность шума квантования (при условии, что импульсы треугольной формы).
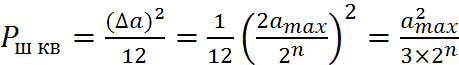
(1)
Коэффициент квантования.
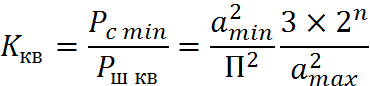
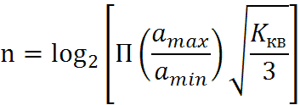
6.2 Использование компандирования в ИКМ.
Источник Непрерывных сообщений
К модулятору передатчика
Квантователь
Компрессор
Кодер
Дискретизатор
На приёме кодовые комбинации подвергаются декодированию, а затем вводятся в экспандер, характеристика которого обратна компрессору.
Приёмная часть.
Приёмник с Демодуля-тором
К получателю
Экспандер
ФНЧ
Декодер
Выигрыш в использовании компандера.
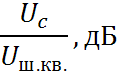
Без компандера.
А
Выигрыш
С компандером.
![]()
![]()
![]()
![]()
7 Случайные процессы.
Случайный процесс – совокупность случайных функций. Случайная функция – функция, значения которой нельзя заранее определить в любой момент времени. Случайная величина – сечение случайной функции(функций). Случайные сигналы – сигналы, математическое описание которых это случайная функция времени.
Рассмотрим абстрактную модель.
Случайные величины
Функция Распределения Вероятностей.
Если только одно сечение, то:
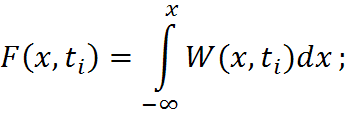
n – мерная ФРВ характеризует распределение в n сечениях.
Функция Плотности Вероятности.
Многомерная ФПВ.
Для n – мерной функции плотности распределения:
Двумерная ФРВ.
Широко используется в технике связи.
![]()
- Невозможное событие.
- Достоверное событие.
- Условие нормировки.
7.1 Числовые характеристики.
Полное описание любого случайного процесса – n – мерная ФРВ, n – мерная ФПВ, но из-за сложности представления и анализа ограничиваются тремя числовыми характеристиками:
1. Математическое ожидание.
Обозначение:
Математическое ожидание – неслучайная величина времени, которая в любой момент является математическим ожиданием данного сечения, то есть это кривая геометрического места точек математического ожидания всех сечений.
2. Дисперсия.
Обозначение:

![]()
Дисперсия – математическое ожидание квадрата отклонения (среднеквадратическое отклонение).
3. Функции корреляции.
Ковариационная функция – математическое ожидание произведения значений случайного процесса в двух сечениях.
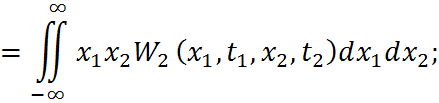
Корреляционная функция определяется для центрированного случайного процесса.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
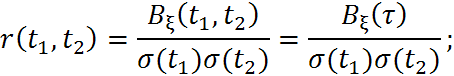
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.