Радиационный баланс земной поверхности Rравен разности по-глощенной солнечной радиации и длинноволнового эффективного излучения:
, /? = Q*(l-<x)-/, (1.12)
где QR— суммарная коротковолновая радиация (сумма прямой и рассеянной радиации); а — альбедо (отношение величины отраженной радиации к величине приходящей радиации); / — эффективное излучение, т. е. разность собственного излучения земной поверхности и поглощаемого на поверхности противоизлучения атмосферы.
Наибольшее значение альбедо характерно для чистого и сухого снега •—0,90—0,95. Однако снежный покров редко бывает совершенно чистым, поэтому средние значения альбедо снега в большинстве случаев равны 0,70—0,80. Альбедо влажного и загрязненного снега снижается до 0,40. Альбедо естественных поверхностей с растительным покровом изменяется сравнительно в небольших пределах — от 0,10 до 0,25.
При большой сухости почвы вся вода, поступающая в виде осад-ков, задерживается молекулярными силами на частицах почвы и в конечном итоге расходуется на испарение. В таких условиях (обычно наблюдаются в пустынях) коэффициент стока уо/хо приближается к нулю. Так как сухость почвы растет с увеличением радиационного притока тепла и с уменьшением количества осадков, то
-^-->0 или -£^-»1 при —------>*э. (1.13)
х0 х0 LxQ
При уменьшении отношения R/Lx0, которое принято называть радиационным индексом сухости, значение zo/xQбудет уменьшаться, т. е. возникнет некоторый сток. При достаточно больших осадках и малом притоке радиационного тепла наступает состояние избыточного увлажнения верхнего слоя почвы. Для условий избыточного увлажнения
Lzo-+Rпри —-------.0. (1.14)
Lx0
Исходя из условий (1.13) и (1.14)
Zo=fthJJT'(1Л5)
где th— символ гиперболического тангенса.
На рис. 1.2 зависимость zo/xoот R/Lx0для значений R/Lx0в соответствии с условием (1.14) изображена прямой О А, для больших R/Lx0в соответствии с условием (1.13) —прямой АВ. Экспериментальные данные показывают, что фактически наблюдается плавный переход от линии О А к линии АВ.
Исследование уравнения связи теплового и водного балансов суши выполнили М. И. Будыко и Л. И. Зубенок (1961). Они проанализировали данные для многих районов суши, для которых испарение было подсчитано по уравнению водного баланса как разность осадков и стока. На рис. 1.3 в общем виде представлена зависимость стока от годовых сумм осадков и радиационного баланса. Исследованиям водного и теплового баланса посвящены работы В. С. Мезенцева, Н. А. Багрова, А. Р. Константинова и др.
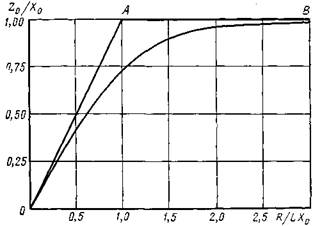
Рис. 1.2. Зависимость коэффициента испарения от радиационного индекса сухости
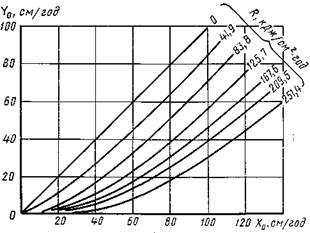
Рис. 1.3. Зависимость стока от осадков и радиационного баланса
На основе уравнений водного и теплового балансов В. С. Мезенцев разработал метод гидролого-климатических расчетов применительно к решению различных задач инженерной гидрологии [24].
Единицы измерения стока воды. Сток в зависимости от решаемой задачи может выражаться в виде расхода воды, объема стока, модуля и слоя стока. Расход воды Q выражается обычно в м3/с Объем стока W— это объем воды, стекающей с водосбора за какой-либо интервал времени Т больше секунды. Следовательно, W=TQ. В таких случаях объем стока выражается в кубических метрах или кубических километрах с указанием, за какой период (месяц, год и , т. д.). Количество воды, стекающей с единицы площади водосбора в единицу времени, называется модулем стока. Выразив модуль стока М в л/(с • км2), получим где F— площадь водосбора, км2. Эта характеристика широко используется в гидрологиче:ких расчетах. Она удобна для сравнения удельной водоносности водосборов рек. Например, для Москвы средний годовой модуль стока равен 6, Хабаровска — 8, Батуми — 50 л/(с-км2).
Если сток сравнивают с осадками и испарением (см. табл. 1.1 и 1.2), говорят о слое стока, т. е. количестве воды, стекающей с водосбора за какой-либо интервал времени, равном толщине слоя, равномерно распределенного по площади этого водосбора (мм/год).
Слой стока у и модуль стока М связаны следующим образом. Объем воды W(м3/год), стекающей с площади водосбора F(км2), составляет:
W=-^—F-W6=WyF. юз
Этот объем воды стекает с водосбора за 31,5-106 с в году
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.