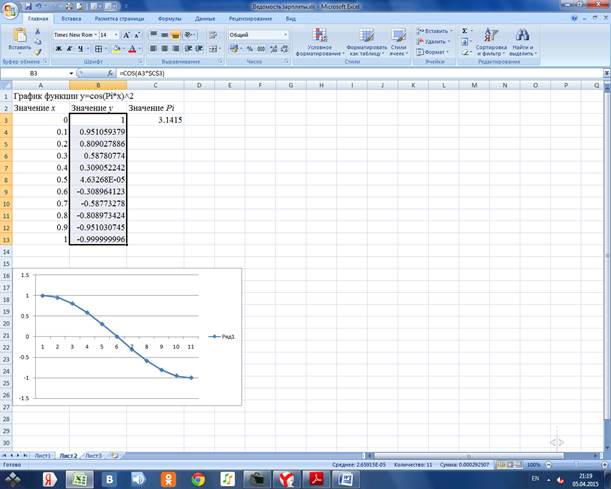
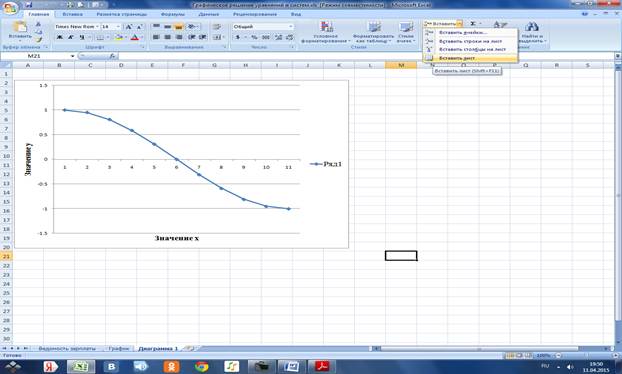
Задание 1. Решить графически уравнение у=cos(Pi*x)˄2
1.1 Находим все значения х внутри данного интервала, где функция у пересекает ось х.
Проводим табуляцию значений х и у
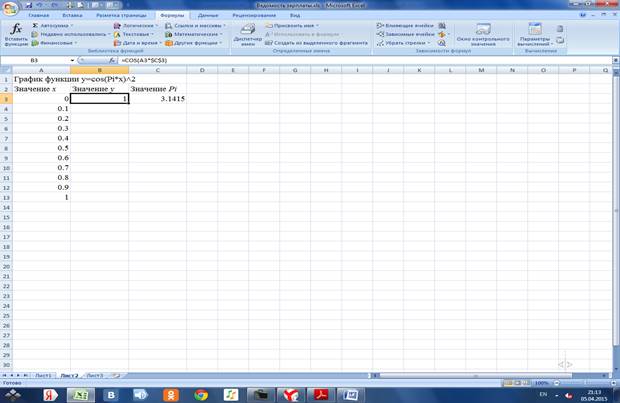
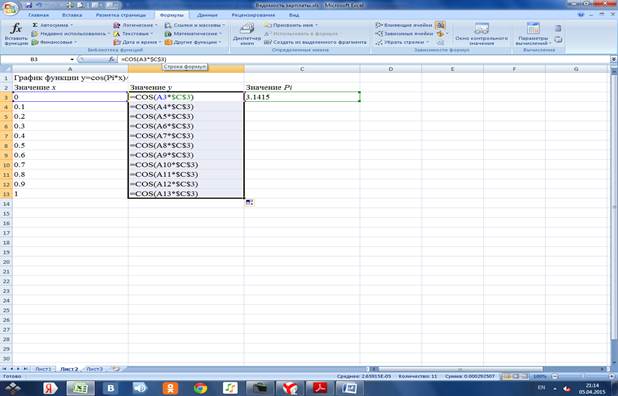
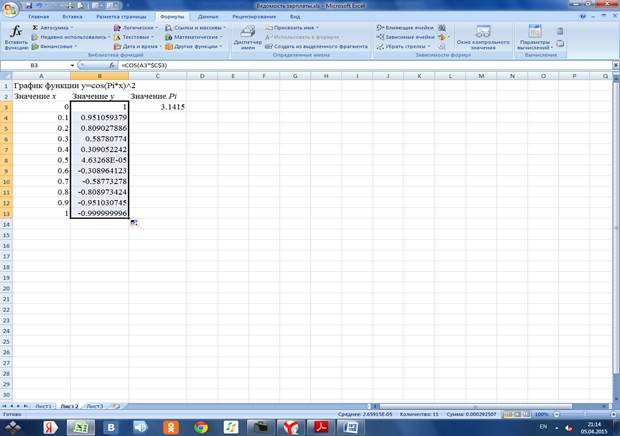
1.2 Строим график функции по диапазону B3:B13
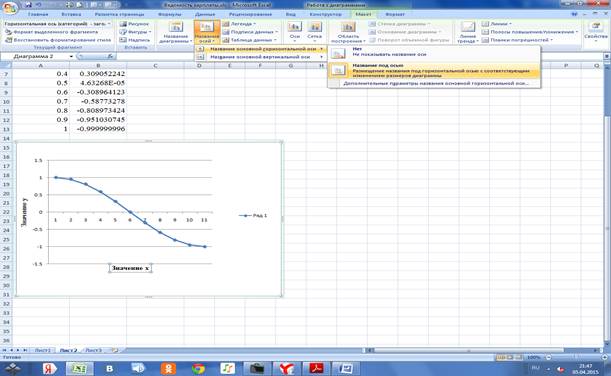
Вводим название осей х и у
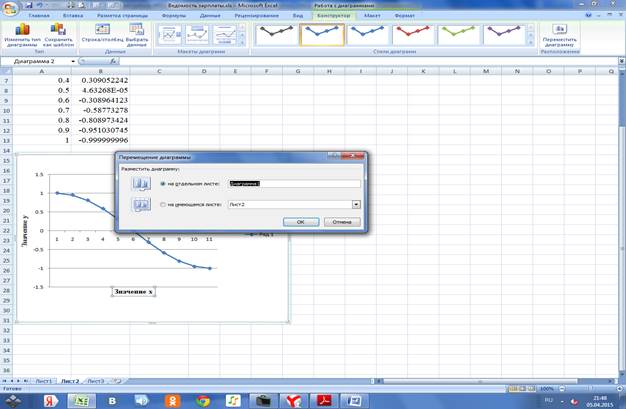
В мастере диаграмм сохраняем диаграмму на отдельном листе
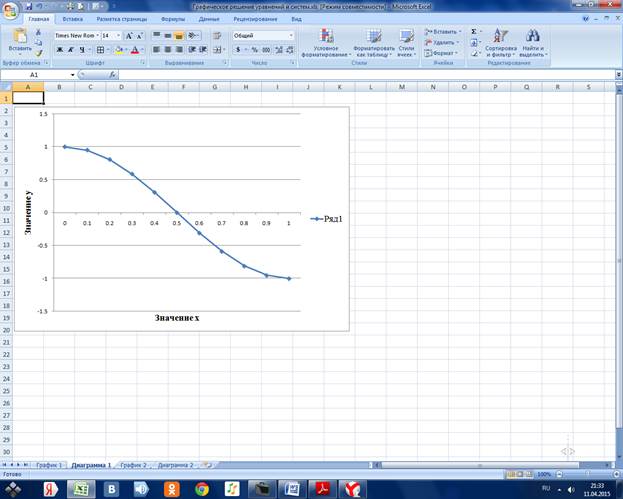
Задание 2. Найти графическое решение уравнения x^3-4*x^2-3*x+6=0
2.1 Открываем новый рабочий лист
2.2 Проводим табуляцию значений аргумента х и функции у1 и у2
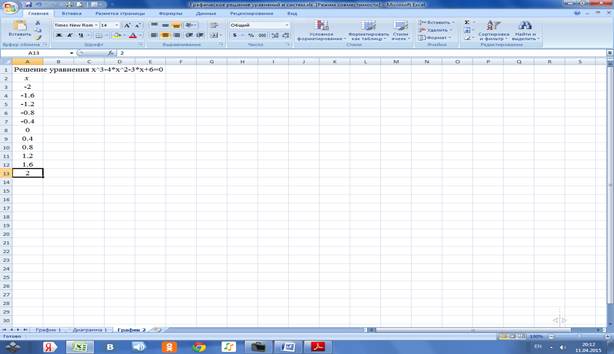
2.2.1 Сводим вычисления в ЭТ, для этого заполняем ячейки А3:А13 значениями х:
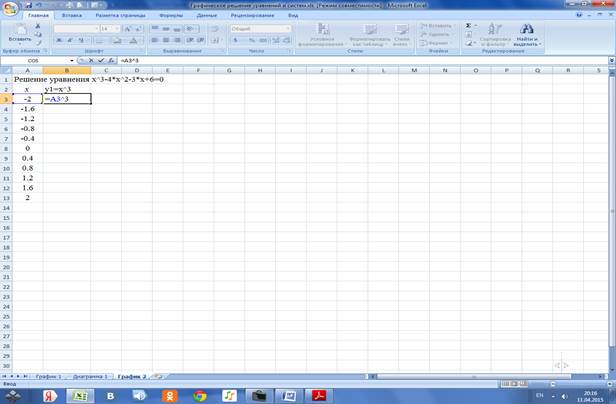
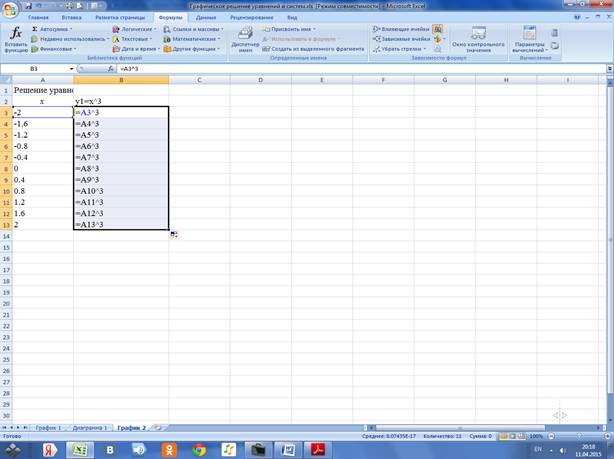
2.2.2 Вводим в ячейку В3 формулу для функции у1=х^3 и копируем её в ячейки В4:В13
2.2.3 Вводим в ячейку С3 формулу для функции у2=4х^2+3х-6 и копируем её в ячейки C4:C13
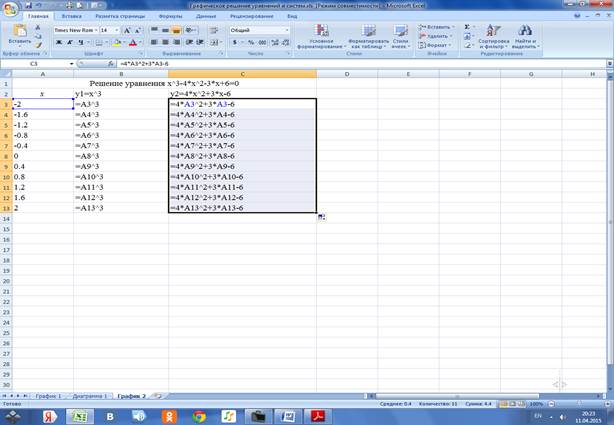
В результате получили таблицу
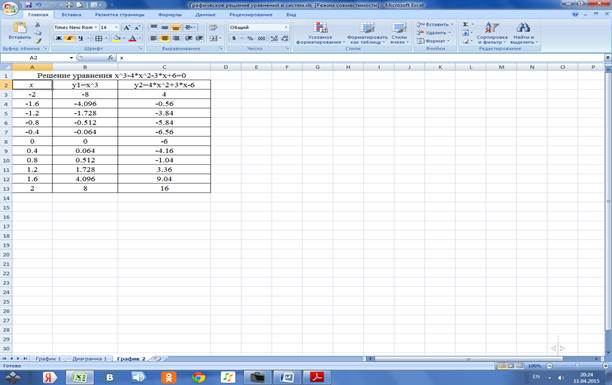
2.3 Строим график функций у1 и у2 на одной диаграмме
2.3.1 Выделяем диапазон данных В3:С13
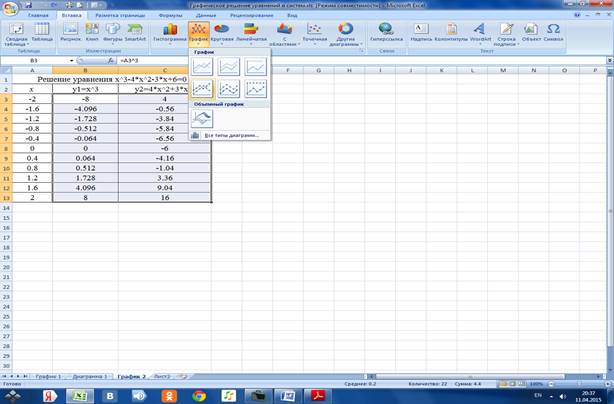
2.3.2 По данному диапазону строим график с маркерами и сохраняем его на отдельном листе Диаграмма 2
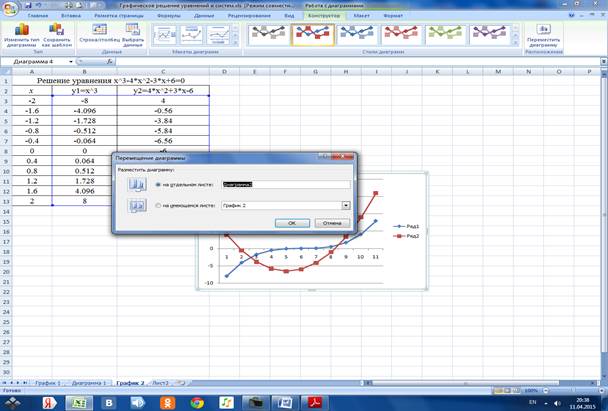
2.3.3 Вводим подписи диапазона данных
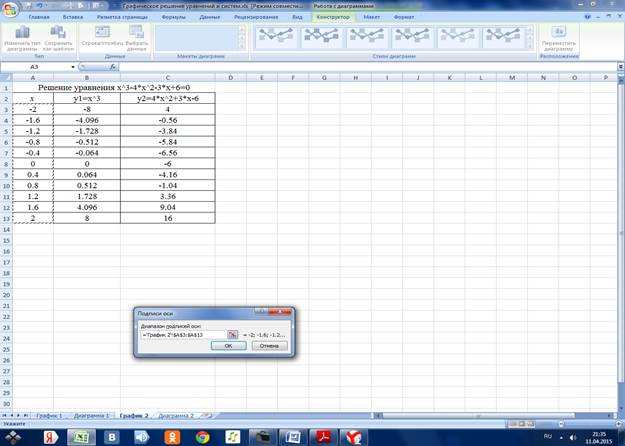
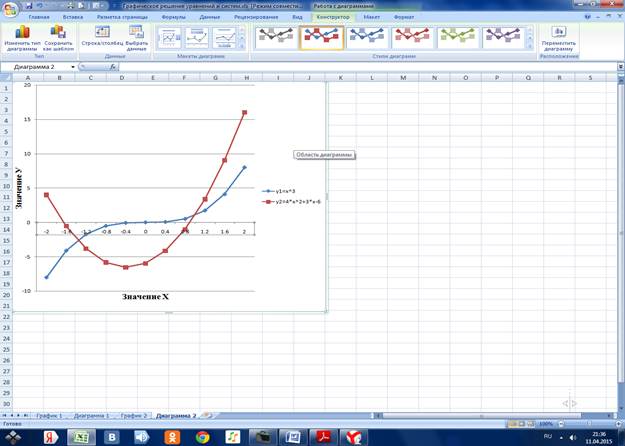
На рассмотренном интервале функции у1 и у2 пересекаются дважды: корни х1=-1,2; х2=1,2.
2.4 Для нахождения третьего корня увеличиваем диапазон до х=5 , т.е. х принадлежит диапазону [-2;5]
2.4.1 Продолжим табуляцию х до ячейки А20. Копируем формулу из ячейки В13 в ячейки В14:В20. Копируем формулу из ячейки С13 в ячейки С14:С20.
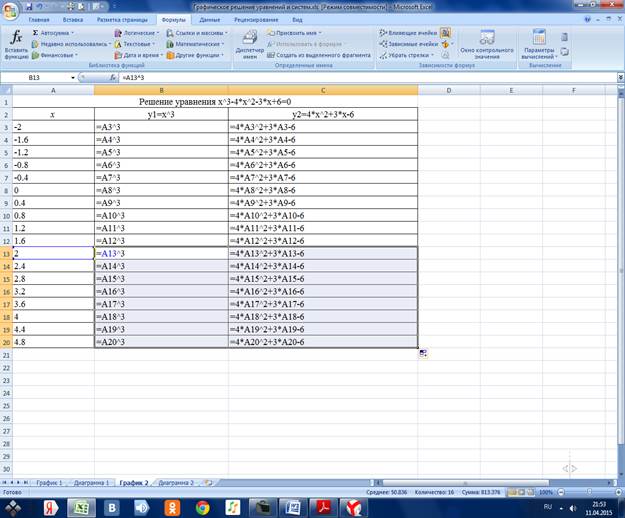
2.4.2 Строим график для этого случая
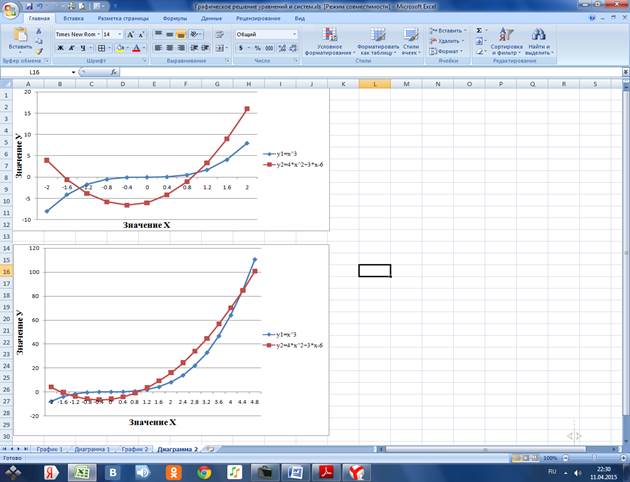
На этом графике функции у1 и у2 пересекаются трижды. Третий корень х3=4,4
Задание 3. Решить графически систему уравнений
![]() в диапазоне x
принадлежит [0;3] с шагом ∆x=0,2
в диапазоне x
принадлежит [0;3] с шагом ∆x=0,2
3.1 Добавляем новый рабочий лист
3.2 Проводим табулирование переменных х, y=sinx; y=cosx
Сводим вычисления в ЭТ:
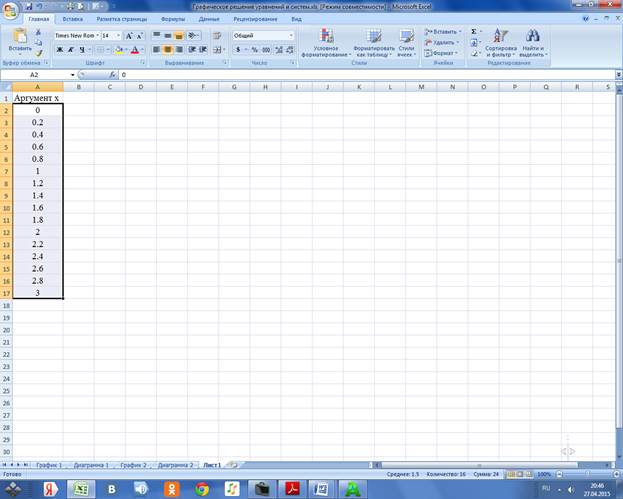
3.2.1 В ячейку А1 вводим заголовок Аргумент х, в ячейку А2 – значение 0, в ячейку А3 – значение 0,2 и проводим табуляцию аргумента х в ячейках А2:А17
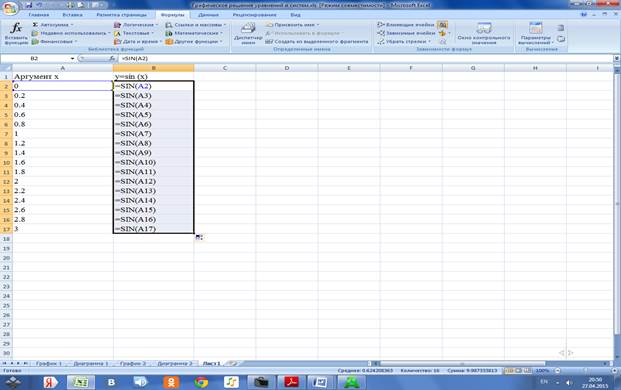
3.2.2 В ячейку В1 вводим заголовок y=sin (x). В ячейку В2 вводим формулу =SIN(A2) и копируем её в ячейки В3:В17
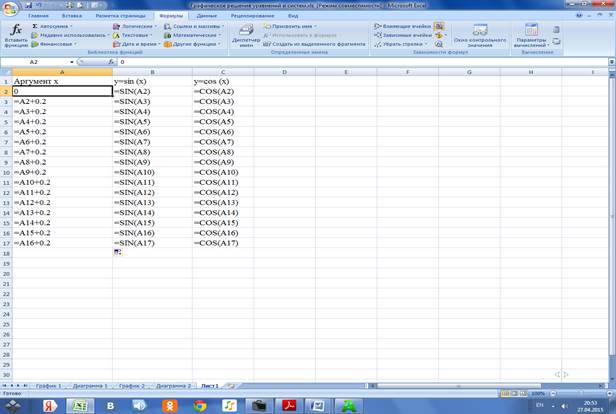
3.2.3 В ячейку C1 вводим заголовок y=cos (x). В ячейку С2 вводим формулу =COS(A2) и копируем её в ячейки C3:C17
3.3 Строим график функций y=sin x, у=cos x на одной диаграмме.
3.3.1 Диапазон для построения В2:C17
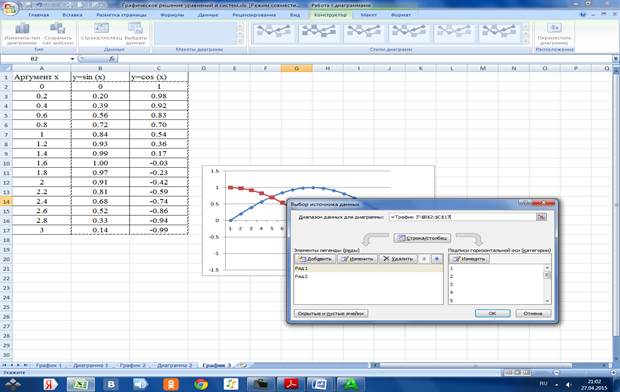
3.3.2 Выбираем название рядов
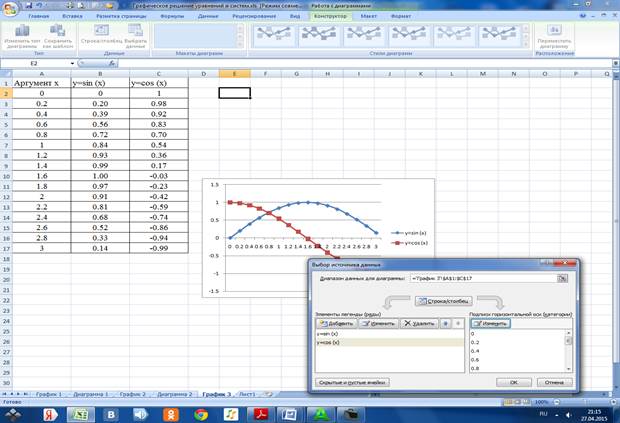
3.3.3 Даем название графику «Система» и осям: ось х – «Аргумент», ось у – «Значения». Сохраняем диаграмму на отдельном листе Диаграмма 3
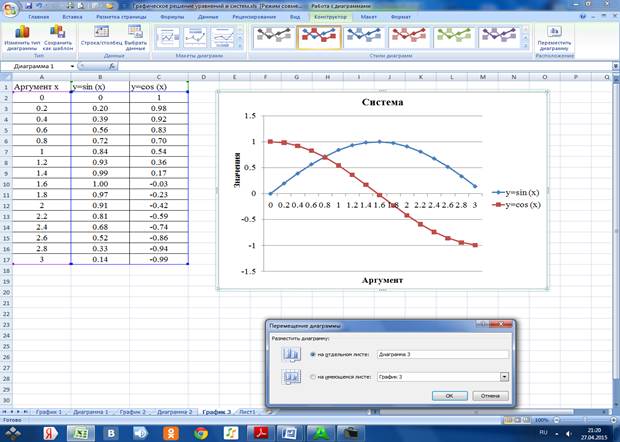
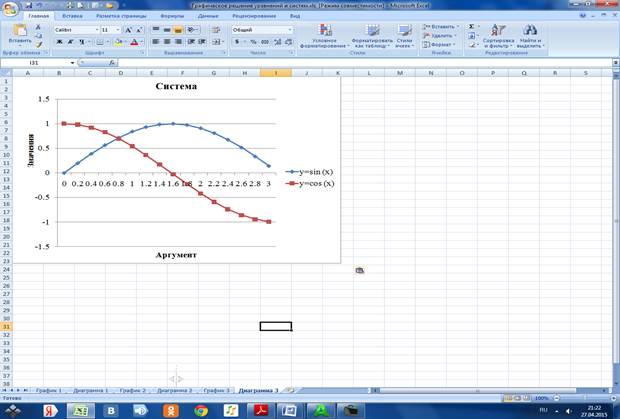
3.3.4 Ставим указатель мыши в точку пересечения графиков.
Ряд «y=cos(x)» Точка «0,8». Значение :0,696706709
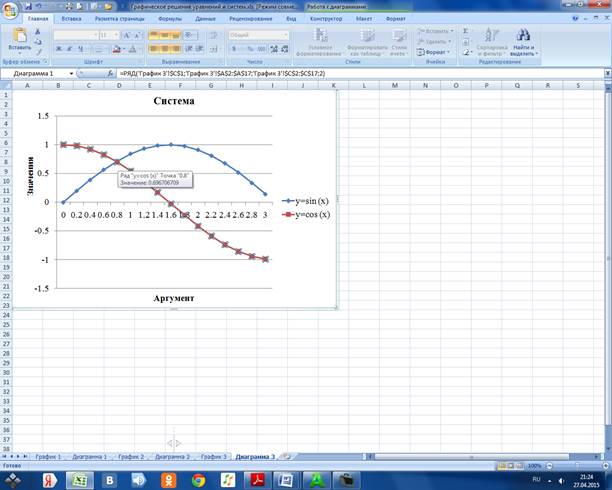
Решением уравнения являются: х=0,8; у=0,697
Задание 4. Решить графически систему уравнений
![]()
в диапазоне x принадлежит [0;2] с шагом ∆x=0,1
4.1 Добавляем новый рабочий лист
4.2 Проводим табулирование переменных х,
![]() ;
y=
x/2
;
y=
x/2
Сводим вычисления в ЭТ
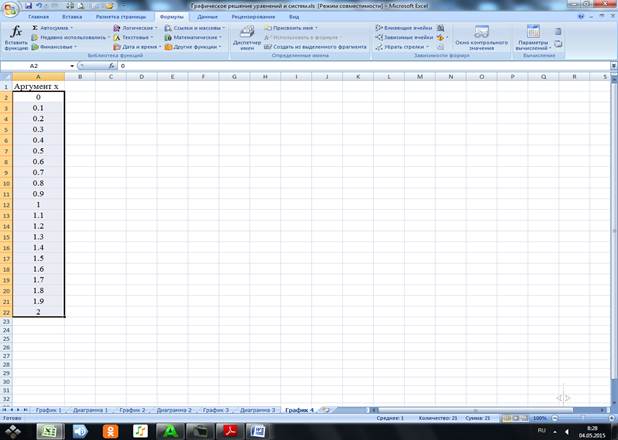
4.2.1 В ячейку А1 вводим заголовок Аргумент х, в ячейку А2 – значение 0, в ячейку А3 – значение 0,1 и проводим табуляцию аргумента х в ячейках А2:А22
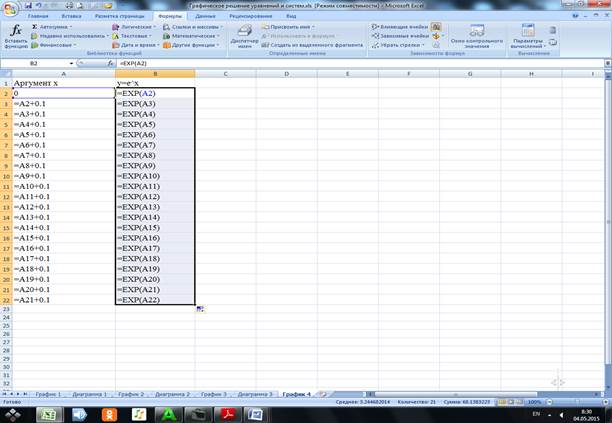
4.2.2 В ячейку В1 вводим заголовок ![]() .
В ячейку В2 вводим формулу =EXP(A2)
и копируем её в ячейки В3:В22
.
В ячейку В2 вводим формулу =EXP(A2)
и копируем её в ячейки В3:В22
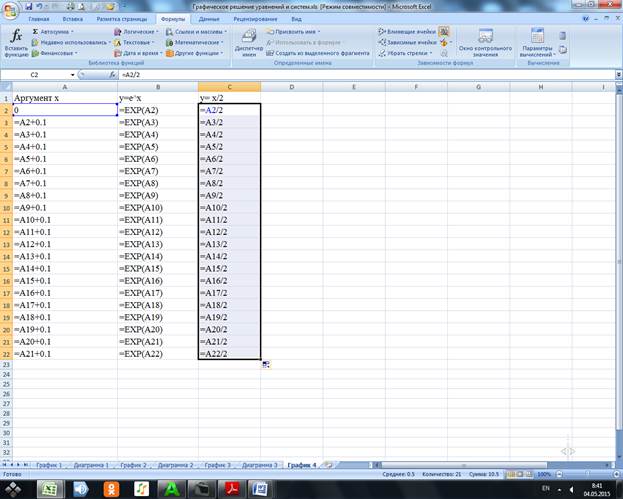
4.2.3 В ячейку C1 вводим заголовок y= x/2. В ячейку С2 вводим формулу =A2/2 и копируем её в ячейки C3:C22
4.3 Строим график функций ![]() ;
y=
x/2
на одной диаграмме.
;
y=
x/2
на одной диаграмме.
4.3.1 Диапазон для построения В2:C22
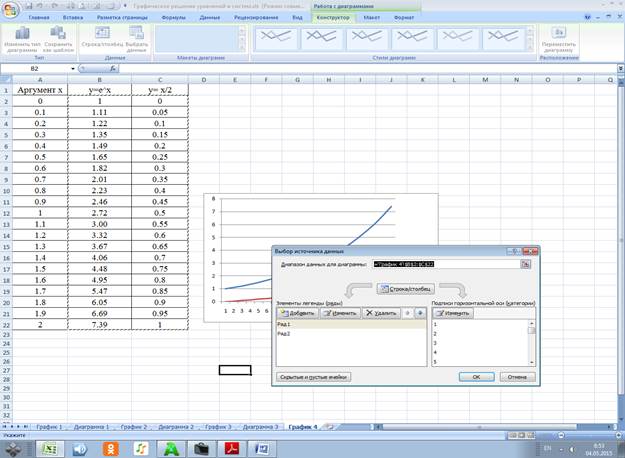
4.3.2 Выбираем название рядов
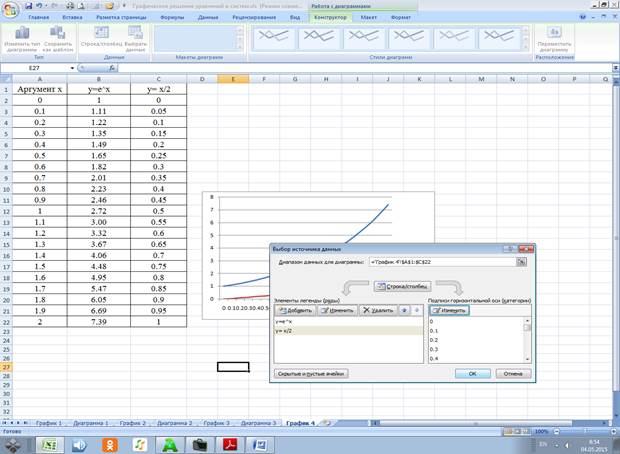
4.3.3 Даем название графику «Система» и осям: ось х – «Аргумент», ось у – «Значения». Сохраняем диаграмму на отдельном листе Диаграмма 3
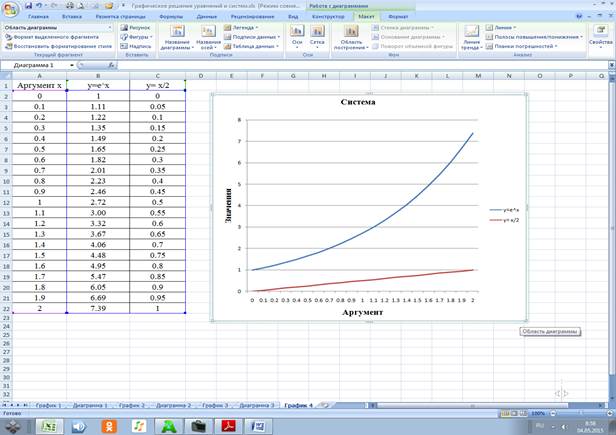
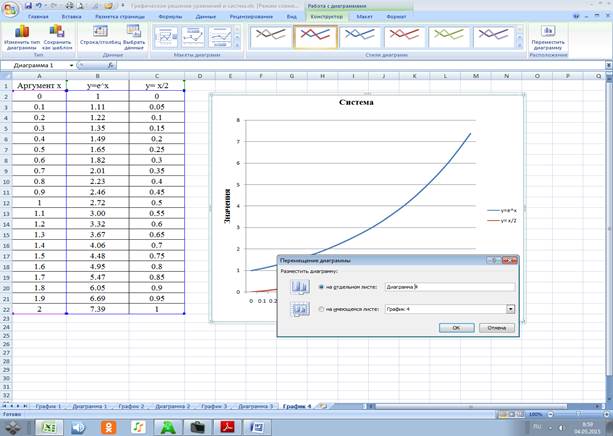
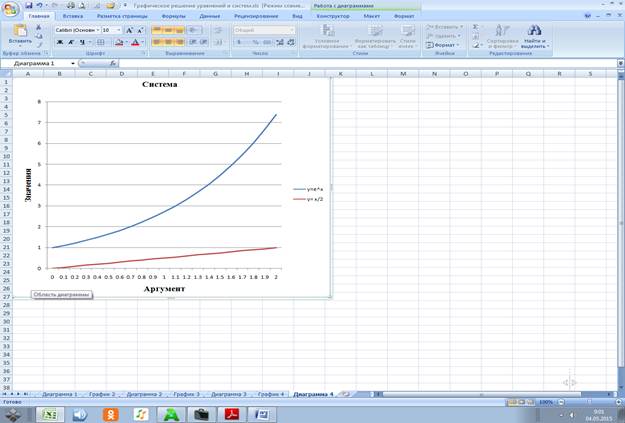
4.3.4 Точка пересечения графиков отсутствует.
Решение системы уравнений
![]()
в диапазоне x принадлежащем [0;2] отсутствует.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.