Основні положення науки про опір матеріалів. Історичний екскурс про формування вчення опору матеріалів як науку. Основні види деформацій конструктивних елементів

Напрямок цих напружень паралельний до осей  та , відповідно, тобто перпендикулярний до поздовжньої осі стержня і дотичний до перерізу. Дотичні напруження діють в площі перерізу і дорівнюють:

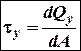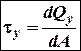;                               .                               (2)

Одиницею виміру напружень є Па, кПа, МПа.

Стан тіла, при якому в тілі виникають напруження або необхідно їх визначити, називається напруженим станом.

Стан тіла, при якому, внаслідок дії зовнішніх сил, тіло деформується, в ньому виникають напруження і необхідно визначити параметри деформування і значення напружень називається напружено-деформованим станом.

2. Переходячи від елементарної площі до повної площі перерізу, з урахуванням формул (1) і (2) ми можемо записати:

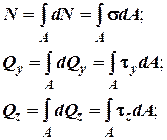
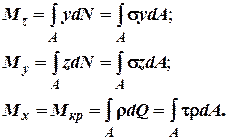                           (3)

Залежності (3) називаються інтегральними рівняннями рівноваги.

При отриманні виразу для крутного моменту у (3) приймалися до уваги наступні перетворення:

3. Оскільки закон розподілу напружень за висотою поперечного перерізу невідомий, вирахувати величину напружень тільки на основі інтегральних рівнянь рівноваги неможливо. Така задача є статично невизначною і для її розв'язку вона розглядається з чотирьох сторін (чотириєдина задача опору матеріалів):

1) Статична сторона задачі, де записуються необхідні інтегральні рівняння рівноваги;

2) Геометрична сторона, в якій оцінюються можливі переміщення точок перерізу, що розглядається. Як правило, це експериментальні дані;

3) Фізична сторона задачі, в якій встановлюється зв’язок між напруженнями і переміщеннями;

4) Проводиться синтез – тобто разом розв'язуються всі рівняння і шляхом виключення або урахування відомих переміщень (деформацій) дістаємо формули, що виражають напруження через зусилля або моменти у перерізі.

4. Розтяг або стиск стержня спричиняють сили, що діють на нього вздовж осі. При цьому, в будь-якому поперечному перерізі за довжиною стержня із шести внутрішніх силових факторів не буде дорівнювати нулю тільки один – поздовжня сила . Тобто ; .

Розглянемо стержень, навантажений зовнішніми силами, які паралельні його поздовжній осі і проходять через центр ваги перерізу. Запишемо для цього стержня чотириєдину задачу.

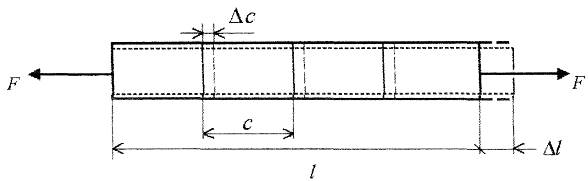
1) Статистична сторона задачі – .

2) Геометрична сторона задачі. При експериментальних дослідженнях було встановлено, що лінії нанесені перпендикулярно до осі стержня при навантаженні стержня переміщуються, залишаючись паралельними одна одній. Передбачаючи, що картина буде незмінною і в середині стержня, прийшли до такого відомого висновку: поперечні перерізи стержня, плоскі до деформації, залишаються плоскими і після її виникнення, переміщуючись вздовж його осі. Цей висновок також має назву гіпотези плоских перерізів. На основі цього, при незмінному навантаженні, можна записати:

3) Фізична сторона задачі полягає у встановленні зв'язку між деформаціями і напруженнями. При експериментальних дослідженнях Робертом Гуком було встановлено, що напруження, які виникають у стержні, прямо пропорційні відносним деформаціям:

,                                                      (4)

де  – коефіцієнт пропорційності, що характеризує фізико-механічні властивості матеріалу. Ця залежність має назву закон Гука. Коефіцієнт пропорційності  у цій залежності носить назву модуля пружності першого роду або модуля Юнга. Найчастіше його також називають модулем пружності. Вимірюється у Па, кПа, МПа і дорівнює:

для сталі:    ;         міді:            ;

алюмінію:  ;         дерева:       .

4) Враховуючи постійність модуля пружності для даного матеріалу (гіпотеза однорідності й ізотропності), закон Гука, а також те, що , знаходимо, що: . Підставляючи цей вираз в інтегральне рівняння рівноваги, отримуємо:

звідки:

.

Тобто, напруження при розтязі-стиску визначаються як відношення поздовжньої сили до площі поперечного перерізу стержня. Знак напружень визначається знаком поздовжньої сили, що діє в перерізі:  – розтяг;  – стиск.

Принцип Сен - Венана

Якщо тіло послідовно навантажувати статично еквівалентними системами сил, то при умови що розміри зони прикладання їх невеликі в порівнянні з розмірами самого тіла, то можна вважати, що в перерізах, достатньо віддалених від місць прикладання навантажень, величина напружень мало залежить від способу навантаження.

Дослідження показали, що на відстані  ( ширина чи діаметр стержня) від точки прикладання сили напруження в перерізі не залежать від характеру її дії.

Визначення деформацій при розтязі і стиску

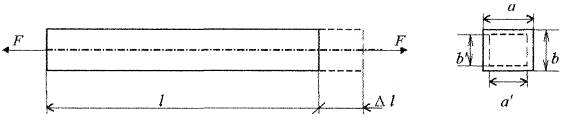
Як відомо:   – абсолютне подовження стержня, або ж абсолютна поздовжня деформація. Має розмірність одиниць довжини;

 – відносна поздовжня деформація;

 – відносна поперечна деформація.

Як показали численні досліди, величина відносної поперечної деформації