Методичні вказівки та завдання до розрахунково-проектувальної роботи з курсу „Опір матеріалів” (спецкурс „Теорія пружності”) на тему ”Використання функції напружень при розв’язанні плоскої задачі теорії пружності та згин пластин”

Методичні вказівки та завдання до розрахунково-проектувальної роботи з курсу „Опір матеріалів” (спецкурс „Теорія пружності”) на тему ”Використання функції напружень при розв’язанні плоскої задачі теорії пружності та згин пластин” для студентів будівельних спеціальностей денної та заочної форм навчання для студентів денної та заочної форм навчання за напрямком підготовки 06.01 – „будівництво”, освітньо-кваліфікаційний рівень – „бакалавр”. – Полтава: ПолтНТУ, 2008. – 16 с.

Укладачі:    Р.В. Толстопятов, кандидат технічних наук, доцент;

                    В.А. Кириченко, кандидат технічних наук, асистент

Відповідальний за випуск:     В.В. Муравльов, кандидат технічних наук, доцент

Рецензенти:   А.М. Пащенко, кандидат технічних наук, доцент;

                        О.Г. Фенко, кандидат технічних наук, доцент

Затверджено науково-методичною радою університету

Протокол  № 4 від 22.05.2008

Коректор   І. Л. Горбушко

Зміст

1 Використання функції напружень при розв’язанні плоскої задачі теорії пружності        4

1.1 Загальні відомості................................................................................................ 4

1.2 Послідовність роботи та рекомендації щодо її написання................................................................................................ 6

1.3 Контрольні запитання................................................................................................ 7

2 Згин пластин        8

2.1 Загальні відомості................................................................................................ 8

2.2 Диференціальні рівняння пружної поверхні та внутрішні сили у декартовій системі координат.................................................................................... 8

2.2 Диференціальні рівняння пружної поверхні та внутрішні сили у полярній системі координат.................................................................................... 9

2.4 Послідовність виконання роботи та рекомендації щодо її написання.............................................................................................. 11

2.5 Контрольні запитання.............................................................................................. 12

Література        12

Додаток А        13

Додаток Б........................................................................................ 14

Додаток В........................................................................................ 16

1 Використання функції напружень при розв’язанні плоскої задачі теорії пружності

1.1 Загальні відомості

Щоб описати зміну форми тіла при його навантаженні і внутрішні сили, які виникають у тілі, використовують такі основні поняття: напруження, деформації, переміщення.

Напруження – інтенсивність внутрішніх сил, тобто величина внутрішніх сил, що припадає на одиницю площі.

Нормальні напруження  виникають у напрямі, перпендикулярному до площадки, а дотичні  – у її площині.

Деформація – відносна зміна розмірів тіла.

Лінійна деформація  – зміна лінійних розмірів, кутова  – зміна кутових розмірів.

Переміщення , ,  – проекції повного зміщення точки на координатні осі.

Щоб повністю описати напружено-деформований стан у довільній точці тіла, необхідно знати шість напружень: , ,, , ,, шість деформацій: , ,, , , та три переміщення: , , .

Але у ряді практично важливих випадків напруження або деформації у напрямі однієї із осей відсутні. Ці випадки називаються відповідно плоским напруженим станом та плоским деформованим станом.

Загальні диференціальні рівняння теорії пружності для плоскої задачі є такими:

– рівняння рівноваги

;

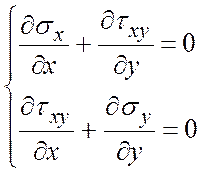– геометричні рівняння

;

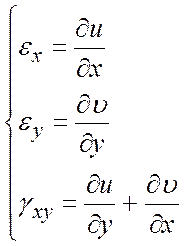– фізичні рівняння:

для плоского напруженого стану

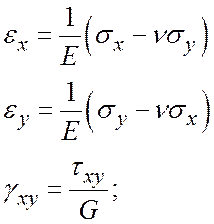
для плоского деформованого стану

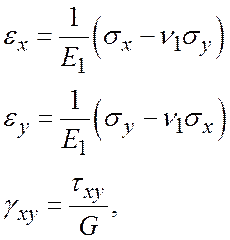
де , , .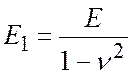

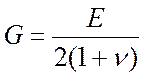Одним із способів розв’язання цих рівнянь є зведення їх до одного рівняння відносно допоміжної функції  – функції напружень:

.

Це рівняння називається бігармонічним рівнянням плоскої задачі, або рівнянням Лапласа.

Функція напружень пов’язана з напруженнями формулами Ері:

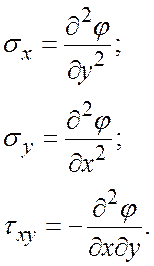
Таким чином, розв’язання плоскої задачі зводиться до знаходження розв’язку бігармонічного рівняння, що задовольняє граничні умови. Зміст граничних умов у даній задачі – пов’язати у точках контуру тіла зовнішні навантаження і напруження. Залежності для граничних умов мають вигляд:

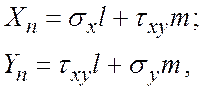
де ,  – проекції зовнішнього навантаження на координатні осі у точці контуру тіла; ,  – напрямні косинуси, тобто косинуси кутів між позитивними напрямками нормалі, яка виходить з тіла й осями координат.

Розв’язування даної задачі у прямій постановці у переважній більшості випадків є неможливим із-за труднощів, пов’язаних із забезпеченням крайових умов. Тому на практиці розв’язується обернена задача – досліджуються функції, які є розв’язком бігармонічного рівняння і визначається, яким зовнішнім навантаженням відповідають ці функції. Якщо є набір функцій напружень і відомі зовнішні навантаження, то при розв’язанні конкретної задачі зовнішнє навантаження можна подати як комбінацію відомих навантажень, а функцію напружень – як комбінацію відомих функцій напружень.

1.2 Послідовність виконання роботи
та рекомендації щодо її написання

У роботі необхідно дослідити, яке поле напружень і які зовнішні навантаження відповідають заданій функції напружень. Для цього потрібно:

– перевірити, чи можна задану функцію напружень використати для розв’язання плоскої задачі;

– знайти вирази для напружень за формулами Ері;

– побудувати епюри напружень у заданих перерізах  та . При цьому, якщо епюра напружень є криволінійною, то треба визначити значення напружень не менше, ніж у 4-х точках за довжиною перерізу;

– визначити зовнішні сили, прикладені на всьому контурі пластини і зобразити їх на рисунку;