Методичні вказівки та завдання до розрахунково-проектувальної роботи з курсу „Опір матеріалів” (спецкурс „Теорія пружності”) на тему ”Використання функції напружень при розв’язанні плоскої задачі теорії пружності та згин пластин”, страница 2

– перевірити рівновагу пластини під дією зовнішніх навантажень.

Варіант індивідуального завдання вибирається із додатка А.

1.3 Контрольні запитання

1.  Що являють собою модуль пружності, модуль зсуву, коефіцієнт Пуассона? Як пов’язані ці величини між собою? В яких одиницях вони вимірюються?

2.  Який матеріал називають ізотропним, анізотропним?

3.  Яка відмінність між плоским напруженим і плоским деформованим станом?

4.  Запишіть основні рівняння для обох видів плоскої задачі?

5.  Яка функція називається бігармонічною?

6.  Поліному якого степеня відповідає однорідний напружений стан?

7.  У чому полягає закон парності дотичних напружень?

8.  Навіщо застосовують функцію напружень?

9.  Як можна розв’язати плоску задачу теорії пружності без застосування функції напружень?

10.  Що являють собою пряма й обернена задача теорії пружності?

11.  Як визначаються напрямні косинуси?

2 Згин пластин

2.1 Загальні відомості

Пластиною називають тіло, в якого один із розмірів (товщина) є значно меншим від двох інших. Задачу про згин пластин зводять до визначення прогинів, внутрішніх сил і напружень. Задача розв’язується методом переміщень, за основну невідому береться функція прогинів  точок серединної площини. Поверхня, на яку перетворюється серединна площина в процесі деформування називається пружною поверхнею пластини. Рівняння цієї поверхні (функція прогинів) визначається рішенням диференціального рівняння четвертого порядку (рівняння Софі-Жермен). Внутрішні зусилля та напруження в пластині визначаються через функцію прогинів. Математичний апарат теорії згину пластин реалізується, як правило, у двох системах координат – декартовій (для прямокутних пластин) та полярній (для круглих симетрично навантажених пластин).

Згин пластин на відміну від балок відбувається у двох напрямках, причому картина згину у цих напрямках буде різною. Інтегральною кількісною характеристикою напружень у пластині є інтенсивність внутрішніх сил – внутрішні сили, що припадають на одиницю ширини перерізу.

2.2 Диференціальні рівняння пружної поверхні
та внутрішні сили у декартовій системі координат

Рівняння Софі-Жермен у декартовій системі координат має вигляд

,                                    

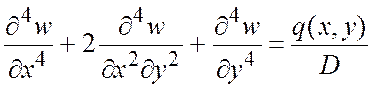де  – інтенсивність розподіленого по площі пластини навантаження;

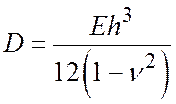 – циліндрична жорсткість пластини Н·м;

,  – модуль пружності та коефіцієнт Пуассона матеріалу пластини;

 – товщина пластини, м.

Внутрішні сили визначаються із функції прогинів за наступними формулами:

                   

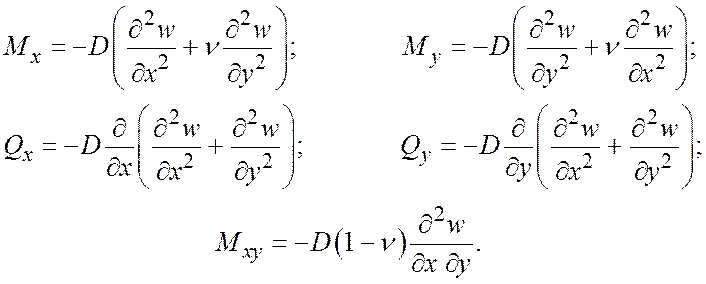
Правила знаків цих внутрішніх сил показані на рис. 1.

Аналітичного розв’язку рівняння Софі-Жермен для декартової системи координат у загальному вигляді не існує, тому, як правило, розв’язують обернені задачі згину прямокутних пластин. При цьому задаються функцією прогинів  і знаходять зовнішнє навантаження та умови закріплення, які відповідають заданій функції.

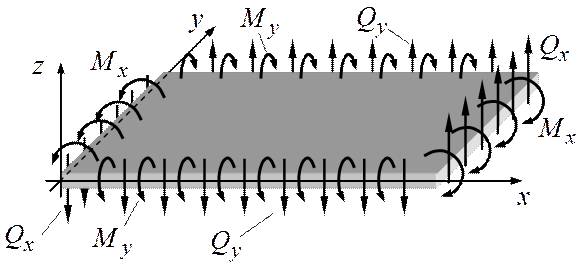
Рисунок 1 – Додатні напрямки внутрішніх сил при згині прямокутної пластини

2.3 Диференціальні рівняння пружної поверхні
та внутрішні сили у полярній системі координат

Рівняння Софі-Жермен у полярній системі координат (тільки у випадку симетричного розміщення опор та навантаження) має вигляд

.                                   

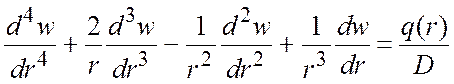Загальний розв’язок цього рівняння існує при , тобто у випадку рівномірно розподіленого по поверхні пластини навантаження. Він має вигляд

,                             

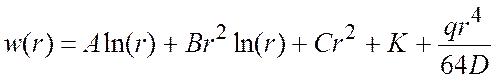де  – константи інтегрування.

Із загального розв’язку можна визначити:

– кут повороту пластини

;                         

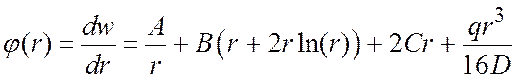– внутрішні сили

;                                                                                                     

;                                                                                                     

.                                                                                                     

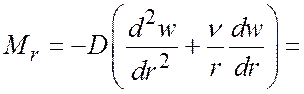
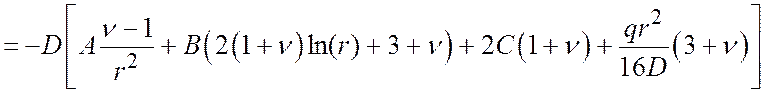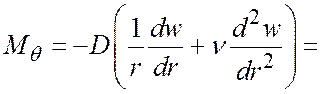
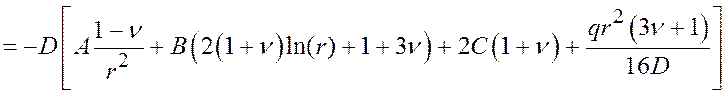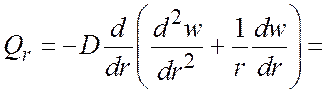
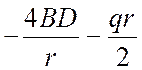Правила знаків цих внутрішніх сил показані на рис. 2.

Константи інтегрування  є сталими для кожної ділянки пластини, де сталою є функція зовнішнього навантаження. Вони у будь-якому випадку можуть бути визначені із кінематичних та статичних крайових умов.

Кінематичними крайовими умовами є:

– умова скінченності прогинів у центрі для суцільної (без отвору) пластини. Із рівняння видно, що при  перший доданок  є скінченним лише при . Таким чином, для суцільних пластин . Другий доданок  при  є невизначеним, проте 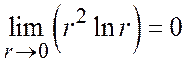, тобто константа  може не дорівнювати 0;

– умова рівності нулю прогинів на шарнірній опорі або прогинів та кутів повороту на абсолютно жорсткій опорі;

– умова рівності між собою прогинів та кутів повороту на межі двох сусідніх ділянок пластини.

Статичними крайовими умовами є взаємозв’язки між внутрішніми силами та зовнішніми навантаженнями на границі пластини.

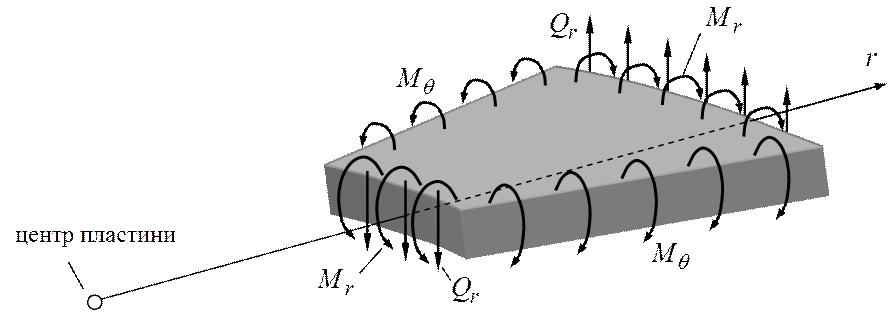
Рисунок 2 – Додатні напрямки внутрішніх сил при згині круглої пластини

2.4 Послідовність виконання роботи
та рекомендації щодо її написання

Для прямокутної пластини.

Визначити умови закріплення (кінематичні крайові умови) та величину прогину , використовуючи задане зовнішнє навантаження  на поверхню пластини. Показати розподіл зовнішнього навантаження на контурі пластини.

Для цього необхідно:

– визначити циліндричну жорсткість пластини;

– перевірити рівність нулю прогинів та кутів повороту на гранях пластини та зобразити схему закріплення;

– шляхом підстановки функції прогинів у рівняння Софі-Жермен визначити константу  через інтенсивність розподіленого по площі пластини зовнішнього навантаження ;

– записати рівняння внутрішніх сил та визначити їх розподіл на незатиснених гранях пластини (для шарнірно обпертих – тільки згинальний момент, для рухомого затиснення – тільки поперечну силу) та зобразити їх на схемі.

Для круглої пластини.

Побудувати епюри прогинів та внутрішніх сил для круглої пластини, знайти максимальні напруження.

Для цього необхідно:

– визначити циліндричну жорсткість пластини;

– записати рівняння прогинів пластини , використовуючи загальний розв’язок;

– записати кінематичні та статичні крайові умови, кількість яких обов’язково повинна дорівнювати кількості невідомих сталих інтегрування;

– розв’язати отриману систему алгебраїчних рівнянь;