7. Случайные процессы

1
1
7. Случайные процессы
-
7.1. Случайные величины и их характеристики.
-
7.2. Случайные процессы.
-
7.3. Случайное блуждание.
-
7.4. Гауссовский случайный процесс.
-
7.5. Стационарные случайные процесс.
-
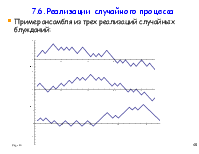
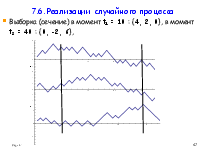
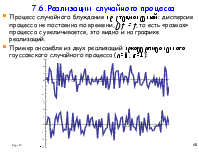
7.6. Реализация случайного процесса.
-
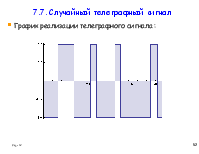
7.7. Случайный телеграфный сигнал.
Page 2
2
7.1. Случайные величины и их характеристики
-
Мы рассматриваем физические явления, зависящий от времени t . Наблюдая явление, мы получаем некоторые числовые данные. Эти наборы данных могут быть детерминированными или случайными. Если, например, на нити раскачивается шарик, то его положение в любой момент времени t вполне определено, его можно описать уравнением колебания и по соответствующей формуле достаточно точно предсказать положение шарика в любой разумный момент времени t. Это детерминированная величина.

Page 3
3
7.1. Случайные величины и их характеристики
-
Существуют явления, исход которых нельзя точно оценить, их числовые параметры нельзя точно предсказать, они не описываются аналитическими формулами или правилами, по которым можно предсказать их значение.
-
Например, количество осадков, которое выпадет завтра. Это недетерминированные (случайные, стохастические) величины. С некоторой погрешностью их можно рассматривать как детерминированные, но применение теории вероятностей (или в зависимости от сути задачи математической статистики) позволяет оценить ошибку их предсказания (риск), которая является числом или случайной величиной.
4
7.1. Случайные величины и их характеристики
-
Случайные величины изучает теория вероятностей и математическая статистика. Различие теории вероятностей и математической статистики состоит в том, что в теории вероятностей случайные величины считаются заданными, например, своими функциями распределения, а математическая статистика на основе экспериментальных данных строит оценки параметров случайных величин. Так, математическое ожидание в теории вероятностей – это число. В математической статистике применяется оценка математического ожидания – это случайная величина, зависящая от данных, полученных в конкретном эксперименте.
Page 5
5
7.1. Случайные величины и их характеристики
-
В теории вероятностей исходное понятие – пространство случайных событий Ω с элементами ω . Элементы ω и их совокупности образуют случайные события. На случайных событиях задается их мера, вес, который называется вероятностью.
-
Кроме вероятности, случайные события (элементы множества Ω и совокупности этих элементов) могут иметь детерминированную числовую оценку. Это, например, может быть выигрыш или проигрыш в рублях в зависимости от случайной раздачи карт.
-
То есть, полученное при раздаче множество карт имеет и вероятность и число (выигрыш), соответствующее множеству и вероятности.
Page 6
6
7.1. Случайные величины и их характеристики
-
Такая числовая оценка является детерминированной, но определена она на случайных событиях. Эта числовая оценка называется случайной величиной. Если пространство Ω конечное, то такие числовые значения можно перечислить и указать их вероятности – это дискретная случайная величина.
-
В математике пространство Ω может иметь бесконечное количество элементов, тогда перечислить все оценки нельзя и для их описания вводятся две функции: функция распределения и функция плотности распределения.
Page 7
7
7.1. Случайные величины и их характеристики
-
Случайная величина задается этими двумя (достаточно одной, любой из них) функциями. Если обозначить через X(ω) случайную величину, определенную на пространстве Ω, то функция распределения FX(x) определяется как
-
функция плотности распределения pX(x) как
-
если производная существует. Если ввести в рассмотре-ние обобщенные функции, в частности δ-функцию и фун-кцию Хевисайда, то функция плотности распределения существуют и для дискретной случайной величины (с.в.).
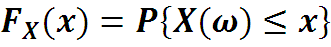
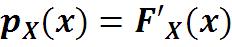
Page 8
8
7.1. Случайные величины и их характеристики
-
Пример. Распределение χ2. Функция плотности распределения положительной случайной величины X(ω) задается формулой
-
где n – число степеней свободы. Найти вероятность того, что значение случайной величины X(ω) меньше, чем 5.
-
Это распределение широко применяется в статистике, например, для построения интервальных оценок параметров,
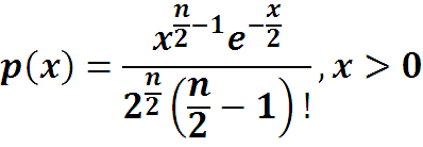
Page 9
9
7.1. Случайные величины и их характеристики
-
для проверки гипотез, например, о том, что параметр случайной величины не превышает фиксированного значения a. Если вывод делается на основе выборки объема m, то число степеней свободы n = m – 1.
-
Вероятность попадания случайной величины X(ω) в интервал [x0, x1] вычисляется по формуле
-
Для нашего примера
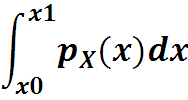
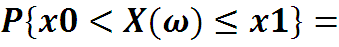
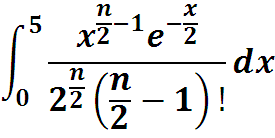
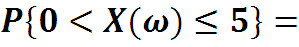
Page 10
10
7.1. Случайные величины и их характеристики
-
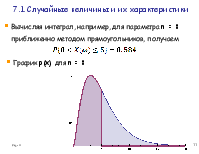
Вычисляя интеграл, например, для параметра n = 8 приближенно методом прямоугольников, получаем
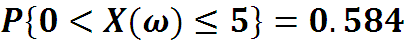
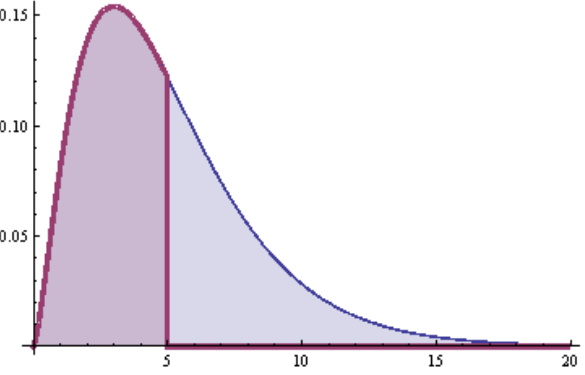
Page 11
11
7.1. Случайные величины и их характеристики
-
Основные числовые характеристики непрерывной случайной величины X(ω) - это математическое ожидание
-
дисперсия
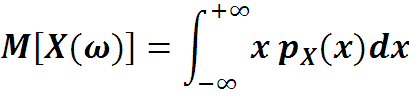
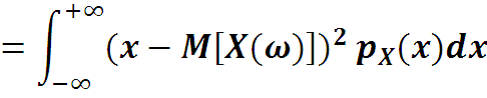
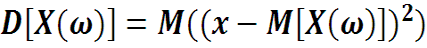
-
и среднеквадратическое отклонение
-
Для простоты будем обозначать эти характеристики mX, DX, σX, или просто m, D, σ (это числа!).
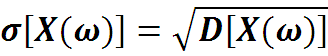
Page 12
12
7.1. Случайные величины и их характеристики
-
Важнейшим в приложениях является нормальное распределение, которое











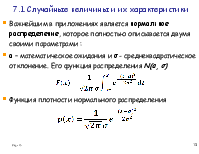
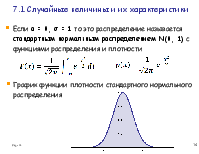
















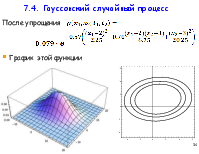





















![]()
![]()
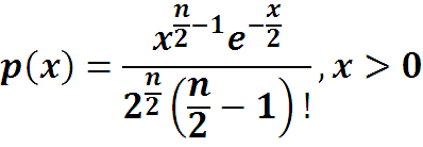
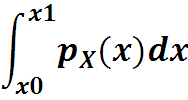
![]()
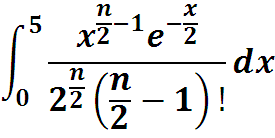
![]()
![]()

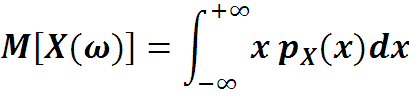
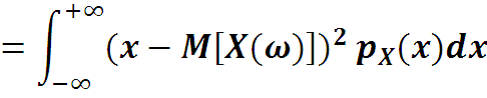
![]()