Задачи о покрытии множеств. Поиск минимальных разбиений, страница 5

7. Поиск минимальных разбиении

Довольно часто решение логических задач связывается с поиском уже не какого-то одного подмножества заданного множества, а некоторой совокупности подмножеств, удовлетворяющей определенным требованиям, и оптимальной в том или ином смысле, например минимальной по числу выбранных подмножеств. Иногда эта совокупность представляет собой разбиение заданного множества на некоторые классы. Примером задачи такого типа может служить широко известная задача о раскраске графа, формулируемая следующим образом.

Задача о   раскраске   г р а ф а. Задан неориентированный граф G = (V, U) с множеством вершин V и с множеством ребер U. Требуется раскрасить его вершины в минимальное число цветов, причем так, чтобы соседние вершины были окрашены в различные цвета.

Поясняющий эту задачу пример приведен на рис. 22, где показаны конкретный граф (а) и минимальная раскраска его вершин (б): номера вершин заменены начальными буквами имен использованных красок (к — красная, с — синяя, з — зеленая). Этот пример достаточно прост и решить его можно вручную, как говорится «эвристически», не утруждая себя использованием или тем более разработкой строгих формальных методов, гарантирующих

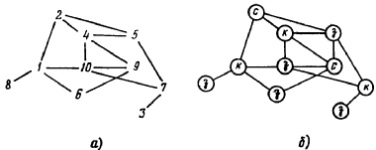Ряс. 22. Неориентированный граф (а) и его минимальная раскраска (б).

оптимальность получаемых решений. Однако нахождение минимальной раскраски более сложных графов представляет собой весьма трудоемкую задачу, решение которой реально только с помощью ЭВМ, а последняя может руководствоваться лишь четко сформулированными правилами поиска. Займемся поэтому соответствующей формализацией.

Простейшим и в то же время наиболее трудоемким является решение задачи «в лоб», заключающееся в переборе всевозможных раскрасок вершин, отсеивании тех из них, в которых нарушается условие разноцветности соседей, и выборе среди остающихся минимальной по числу использованных красок. Однако этот метод явно неразумен — уж очень много приходится перебирать вариантов раскраски: до сⁿ, где n — число вершин, а с - число используемых красок.

Более практично свести эту задачу к задаче о кратчайшем покрытии. Для этого следует отыскать все максимальные пустые подграфы графа G (пустым называется граф без ребер) и построить матрицу бинарного отношения принадлежности вершин графа G этим подграфам. После нахождения кратчайшего покрытия этой булевой матрицы остается выбрать образующие его подмножества вершин, т. е. некоторые из максимальных пустых подграфов, и устранить возможные пересечения между ними. Полученное таким образом разбиение множества V представит искомое решение: вершины каждого класса окрашиваются в свой цвет.

Этот метод гарантирует нахождение минимальной раскраски, однако обладает своими недостатками, связанными с необходимостью построения матрицы указанного бинарного отношения, которая может оказаться слишком громоздкой.

Рассмотрим в связи с этим другой способ раскраски графа, позволяющий избежать построения промежуточной матрицы и поиска ее кратчайшего покрытия, но также гарантирующий получение оптимального решения. При этом способе выполняется некоторая последовательность довольно простых действий — элементарных шагов, изменяющих текущую ситуацию путем ее редуцирования или расщепления. Таким образом, мы будем иметь дело с некоторым методом комбинаторного поиска. Уточним его.