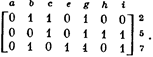Задачи о покрытии множеств. Поиск минимальных разбиений, страница 3

Затем выбираются строка 10  и  столбец  d,             а  матрица           сокращается до

Следующий выбор строки 2 и столбца g приводит к получению покрытия {d, f, g}. В данном случае оно оказывается кратчайшим.

Гарантия того, что полученное покрытие действительно будет кратчайшим, может быть выдана лишь алгоритмом комбинаторного поиска, организующим некоторый достаточный для этого перебор, который может оказаться весьма трудоемким. Существенное сокращение этого перебора обеспечивается на основе формулируемых ниже правил редуцирования переменной матрицы X, характеризующей текущую ситуацию. Данные правила применимы в тех ситуациях, когда некоторые два столбца или две строки матрицы Х находятся в отношении поглощения. Это отношение определяется следующим образом: булев вектор а поглощает булев векторb, если каждая пара одноименных компонент a_i и b_i удовлетворяет условию a_i >= b_i, т. е. не может быть, чтобы a_i = 0 и b_i = 1.

Правило удаления строки. Из матрицы Х удаляется строка x_i , если она поглощает некоторую другую строку  x_j .

Правило удаления столбца. Из матрицы Х удаляется столбец хⁱ , если он поглощается некоторым другим столбцомx^j .

Первое из этих правил универсально в следующем смысле: требования, предъявляемые к покрытию со стороны строки x_i , будут полностью удовлетворены при удовлетворении требований строки x_j . Следовательно, строка x_i оказывается излишней.

Второе правило имеет более частный характер. Удаляя столбец хⁱ мы тем самым отказываемся включать ею в искомое покрытие. Этот отказ оправдывается следующим рассуждением: если существует некоторое кратчайшее покрытие со столбцом xⁱ то, заменив xⁱ на x^j , мы получим другое покрытие, которое также будет, кратчайшим. Таким образом, удаляя из рассмотрения столбец xⁱ мы не теряем возможности найти одно из кратчайших покрытий. Возможность нахождения некоторых из кратчайших покрытий при этом теряется, но это не должно нас волновать, так как для нас достаточно найти лишь одно из них.

Наряду с актами редуцирования матрицы Х в число элементарных шагов включаются приращения конструируемого покрытия.

Правило приращения покрытия. Если некоторая строка x_i матрицы Х имеет лишь один элемент x_i^j со значением 1, то столбец x^j включается в конструируемое покрытие.

Естественно, что включаемые в покрытие столбцы удаляются из матрицы Х вместе со всеми покрываемыми ими строками, в которых они содержат единицы.

Сформулированные правила редуцирования позволяют последовательно упрощать переменную матрицу X, выбрасывая из нее поглощающие строки и поглощаемые столбцы, и искать затем кратчайшее покрытие остатка исходной матрицы С — некоторого ее минора. Если в очередном миноре нет ни поглощающих строк, ни поглощаемых столбцов, следует применять правило расщепления, представляющее собой обобщение правила приращения покрытия.

Правило расщепления. В матрице Х отыскивается минимальная (по числу единиц) строка и поочередно рассматриваются варианты, связанные с включением в конструируемое покрытие столбцов, имеющих в этой строке единицу.

Дополнительное сокращение перебора обеспечивается следующим правилом ограничения, или правилом возврата.

Правило возврата. Если в процессе поиска решения удалось найти некоторое покрытие, последующий перебор ограничивается рассмотрением таких подмножеств из В, мощность которых меньше мощности найденного покрытия.

Рассмотрим работу сформулированных правил на старом примере.

Демонстрация алгоритма. В исходной ситуации принимается, что Х_o=С, а конструируемое покрытие пока пустое. В матрице Х удаляется строка 1, поскольку она поглощает строку 9, и строка 3, поглощающая строку 10. В полученном миноре выбрасывается столбец а, так как он поглощается столбцом d. Получается не упрощаемый далее минор