Задачи о покрытии множеств. Поиск минимальных разбиений, страница 4

Выберем теперь строку 4, первую из минимальных по числу единиц. Она содержит единицы в столбцах d и e, в соответствии с чем предстоит рассмотреть два варианта расширения конструируемого множества: включение в него элемента d или отказ от этого и, следовательно, включение элемента e. Анализируя первый вариант, мы удаляем как столбец d, так и покрываемыеим строки 4, 8 и 10 и рассматриваем далее остаток матрицы

Затем выбрасываются поглощаемые столбцы с, e, i и поглощающая строка 2, в результате чего получаем

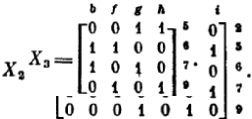Производится расщепление по строке 5. Включение в решение элемента g приводит к удалению покрываемых им строк 5 и 7, а также к последующему выбрасыванию поглощаемых столбцов b и h. Очередной минор элементарен:

Становится очевидным, что в решение следует включить единственный оставшийся элемент f. Таким образом получаем покрытие {d, g, f}, содержащее три элемента. Запомним пока его.

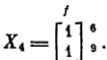В дальнейшем есть смысл продолжать поиск покрытий только среди таких подмножеств из В, которые состоят не более чем из двух элементов. Возвращаясь к предшествующей точке ветвления вариантов, мы вновь рассматриваем минор Х₃ и выбираем теперь оставшийся вариант покрытия строки 5, по которой производилось расщепление, т. e. выбираем столбец h . Испытывая получаемое при этом подмножество {d, h}, убеждаемся, что оно не является покрытием, например им не покрывается строка 6. В связи с этим возвращаемся к рассмотрению ситуации, характеризуемой матрицей X₁. В этой ситуации

расщепление производилось по строке 4. Теперь в качестве первого элемента решения выбираем не d, a e и выбрасываем его и покрываемые им строки 4 и 7, Удаляется также столбец d,соответствующий уже рассмотренному варианту, после чего мы переходим к рассмотрению матрицы

Далее выбрасывается строка 5 и столбец g. В полученной матрице

для покрытия строки 10 необходимо включить в решение элемент i. Однако после этого потребуется обеспечить покрытие остатка

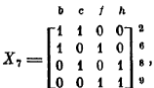для чего испытываемое подмножество {е, i} придется расширить. Отсюда заключаем, что покрытия мощностью менее трех не существует. Следовательно, найденное ранее покрытие { d , g , f } является кратчайшим.

Проведенные рассуждения представляются более компактно схематически в виде дерева поиска, изображенного на рис. 20, где точки ветвления рассматриваемых вариантов отмечены кружками. В последних заключены номера строк, по которым производится разложение, а исходящие из них дуги отмечены символами выбираемых столбцов. Дуги нагружены также метками выполняемых действий: показана последовательность рассматриваемых миноров и способ получения их друг из друга — перечислены удаляемые столбцы и строки. Номера ярусов дерева совпадают с мощностью испытываемых подмножеств из В.

Отбросив информацию об однозначных операциях редуцирования, не связанных с ветвлением вариантов, можно существенно упростить вид дерева поиска (рис. 21). Производимый при поиске перебор оказывается в данном случае мизерным: он ограничен двумя точками ветвления, с коэффициентом 2 в каждой из них.  Рассмотренный пример оказался, таким образом, довольно простым. Однако объем вычислений быстро возрастает с увеличением размеров исходной булевой матрицы. В этом случае для решения задачи могут быть рекомендованы   дополнительные приемы. Рассмотрим, например, ситуацию, когда ищется покрытие .мощностью не свыше k (допустим, что некоторое покрытие мощностью k+ 1 уже найдено ) и анализируется очередной минор на глубине L , где испытываются подмножества из В мощностью L. Очевидно, что в этой ситуации следует ограничиться проверкой лишь таких добавок к испытываемому подмножеству, мощность которых не превосходит k - L . Если k- L = 1, можно обращать внимание лишь на столбцы, состоящие сплошь из единиц, если k-L=2, производится поиск таких пар столбцов, покомпонентная дизъюнкция которых дает столбец без нулей, и т. д.