Классические методы минимизации булевых функций. Сжатие булевой матрицы, страница 5

Метод основан на применении операции обобщенного склеивания, которой подвергаются любые два смежных вектора, представляющие соответствующие элементарные конъюнкции, входящие в преобразуемую ДНФ. Продуктом обобщенного склеивания смежных векторов u и v служит троичный вектор, принимающий значение «—» в той компоненте, по которой u и v ортогональны, а также там, где оба вектора имеют значение «—», и принимающий значение 0 или 1 в остальных компонентах, причем это значение совпадает там со значением одного из векторов u и v. Например, продукт обобщенного склеивания смежных векторов

и

определяется каквектор

1—0—11.

Метод Блека — Порецкого заключается в чередовании операций обобщенного склеивания (с включением получа-

Склеивания (с включением получаемых при этом продуктов в преобразуемую ДНФ) и операций поглощения (при которых поглощаемые члены исключаются из ДНФ). Процесс заканчивается, когда после очередной операции оказывается, что в ДНФ отсутствуют члены, находящиеся в отношении поглощения, и для каждой пары смежных членов в ДНФ будет присутствовать член, поглощающий продукт их обобщенного склеивания. В этом случае полученная ДНФ будет сокращенной.

Продемонстрируем метод на следующем примере, когда булева функция f задана матрицей

Перебор пар элементов некоторого расширяющегося множества разумно производить в следующем порядке:2—1, 3—1, 3—2, 4—1, 4—2, 4—3 и т. д. Реализуя этот перебор в данном случае, мы не находим поглощающих строк, но отыскиваем пары смежных строк 2—1,3—1, 4—2, 4—3 и дополняем ДНФ продуктами соответствующих обобщенных склеиваний:

 Продолжая перебор пар (5—1, 5—2 и т. д.), мы находим пары смежных строк 5—4, 6—5, 7—1, 8—7 и обнаруживаем, что строка 7 поглощает строку 2. Исключим поглощаемую строку и получим продукты обобщенного склеивания

Однако оказывается, что каждая из этих строк поглощается некоторой из предыдущих, в связи с чем их не следует включать в конструируемое множество. В результате получаем матрицу удовлетворяющую сформулированному ранее требованию: строки не поглощают друг друга и при обобщенном склеивании смежных строк образуются строки, поглощаемые уже имеющимися в матрице. Следовательно, полученная матрица представляет сокращенную ДНФ рассматриваемой булевой функции.

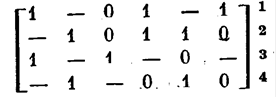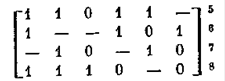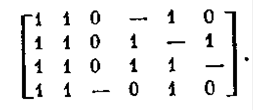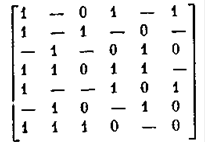Далее делается то же, что и в методе Квайна — Мак-Класки: строится матрица К и находится ее кратчайшее покрытие. При этом придется все-таки предварительно построить совершенную ДНФ или эквивалентное ей характеристическое множество рассматриваемой булевой функции.

Необходимость получения в явном виде множества А всех простых импликант булевой функции f и множества В всех членов совершенной ДНФ этой функции приводит к существенным ограничениям, характерным для рассмотренных методов. Мощности данных множеств, как правило, быстро растут с ростом числа аргументов функции f, и таблица Квайна может стать слишком громоздкой, чтобы можно было надеяться на практическое ее построение и нахождение ее кратчайшего покрытия.

В связи с этим представляют несомненный интерес методы нахождения не оптимального решения — кратчайшей или минимальной ДНФ,— а некоторого хорошего приближения к нему. Будем называть условно такие методы приближенными. Можно предложить также несколько «точных» методов, гарантирующих получение оптимальных решений в некоторых частных ситуациях, представляющих практический интерес, когда рассматриваемая булева функция ограничена по некоторому параметру.Такие методы будут рассмотрены ниже,

15. Сжатие булевой матрицы