Классические методы минимизации булевых функций. Сжатие булевой матрицы, страница 4

В этой матрице соседними оказываются строки 1 и 6, 1 и 9, 2 и 3 и т. д. Склеивая их, мы получим следующее множество строк, содержащих по одному значению «—» и представляющих соответственно элементарные конъюнкции (n-1)-го ранга (в рассматриваемом случае n = 6):

(слева показаны номера склеиваемых строк)

.

Оказывается, что все строки исходной матрицы, кроме строки 11, поглощаются некоторыми из новых строк и, следовательно, удаляются. После этого аналогичные операции склеивания осуществляются уже над строками (п - 1)-го ранга, что приводит к получению строк:

Заметим, что каждая из этих строк получена при этом в двух экземплярах (вообще, при использовании описываемого метода каждая из строк (n - k)-гo ранга появляется в k экземплярах). В данном случае оказывается, что новые строки (n- 2)-го ранга поглощают все строки (n - 1)-го ранга. Поскольку среди них нет соседних строк, процесс получения новых строк прекращается. Устраняя поглощаемые строки и оставляя по одному экземпляру среди остающихся, получим сокращенную ДНФ в ее матричной форме строкам которой для удобства присвоены индивидуальные имена.

Итак, из исходного множества членов совершенной ДНФ булевой функции f мы получили множество членов сокращенной ДНФ. Обозначив первое из этих множеств через В, а второе через А, построим так называемую таблицу Квайна ¾ булеву  матрицу К, задающую бинарное отношение формальной импликации между элементами этих двух множеств: k^j_i=1, если b_jÞa_i, и k^j_i=0 в противном случае

Столбцы матрицы К соответствуют членам совершенной ДНФ и, следовательно, тем наборам значений аргументов, на которых функция f принимает значение 1, строки — членам сокращенной ДНФ, т. е. подмножествам таких наборов, образующих максимальные интервалы характеристического множества М¹ и соответствующих простым импликантам. Формируя из этих импликант функции f некоторую ее ДНФ, нам надо побеспокоиться о том, чтобы для каждого из элементов множества М¹ в ДНФ нашелся член, принимающий на нем значение 1. Это означает, что из матрицы К надо выбрать совокупность строк, образующих покрытие этой матрицы. Стремясь получить кратчайшую ДНФ, мы должны найти кратчайшее строчное покрытие булевой матрицы К.

Эта уже знакомая нам задача решается для данной матрицы легко, поскольку ряд столбцов в матрице содержит лишь по одной единице, и, следовательно, выбор соответствующих им строк, содержащих эти единицы, обязателен. Такими оказываются все строки, кроме Б. Они образуют покрытие, являющееся единственным кратчайшим строчным покрытием матрицы К. Так получается ДНФ, составленная из отобранных описанным образом простых импликант:

Алгебраической интерпретацией этой ДНФ служит   а формула:

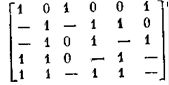Описанный метод прост и алгоритмичен, однако оказывается довольно трудоемким, даже если он реализуется на ЭВМ. При конструировании множества всех простых импликант много времени тратится на поиск соседних элементарных конъюнкций в преобразуемой ДНФ. Чтобы сократить производимый при этом перебор анализируемых пар конъюнкций, МакКласки предложил группировать представляющие их строки не только по рангу, но также по числу единиц, с тем чтобы ограничиться затем рассмотрением таких пар строк, одна из которых содержит на одну единицу больше, чем другая. Нетрудно убедиться в том, что только такие строки могут быть соседними.

М е т о д   Б л е к а—П о р е ц к о г о. Если функция f задана некоторой ДНФ произвольного вида, то для применения метода Квайна — МакКласки ее надо предварительно преобразовать к совершенной форме, что может быть не всегда удобно. Более целесообразным в этом случае может оказаться использование метода Блека — Порецкого.