Классические методы минимизации булевых функций. Сжатие булевой матрицы, страница 3

М е т о д  К в а й н а — М а к К л а с к и. Этот метод предполагает, что функция f задана первоначально  в  совершенной ДНФ, составленной из полных элементарных конъюнкций, каждая из которых содержит символы всех переменных. Такую форму легко получить из таблицы значений функции f, поскольку каждый член совершенной ДНФ соответствует некоторому набору значений аргументов, на котором функция f принимает значение 1. При матричном представлении совершенной ДНФ эти наборы будут непосредственно заданы строками матрицы.

Метод основан на применении двух операций, называемых по традиции операциями склеивания и поглощения и выполняемых над некоторыми парами членов преобразуемой ДНФ, пока эта ДНФ не превратится из совершенной ДНФ в так называемую сокращенную ДНФ, представляющую собой дизъюнкцию всех простых импликант. Нам будет удобнее определить эти операции над троичными векторами, представляющими интервалы булева пространства аргументов x₁, x₂, … , x_n  и соответствующие им элементарные конъюнкции.

Рассматривая два троичных вектора u и v с равным числом компонент, введем для начала некоторые отношения, в которых они могут находиться. Стандартным образом определим отношение равенства u = v , как покомпонентное. Векторы u и v ортогональны (u ort v), если в некоторой паре одноименных компонент один из этих векторов имеет значение 0, а другой — значение 1 (будем говорить в порядке уточнения, что векторы ортогональны по этой компоненте). Если при этом значения остальных компонент попарно равны, векторы u и v находятся в отношении соседства (u nei v). Обобщением отношения соседства служит отношение смежности: векторы u и v смежны (u adj v), если они ортогональны ровно по одной компоненте. Наконец, введем отношение

поглощения,оказывающееся, не в пример предыдущим, несимметричным. Вектор u поглощает вектор v (u abs v), если значения его компонент, отличные от «—», совпадают со значениями одноименных компонент вектора v. Строгости ради заметим, что «если» понимается в этих определениях как «если и только если».

Приведем примеры векторов, находящихся в данных отношениях:

Будем теперь рассматривать троичную матрицу U как некоторую произвольную ДНФ булевой функции f. Если в этой матрице существует некоторая пара соседних строк, то их можно «склеить», образовав новую строку путем передачи ее компонентам совпадающих значений и присвоения значения «—» той компоненте, по которой соседние строки ортогональны. Например, продукт склеивания соседних строк

и

будет представлен строкой

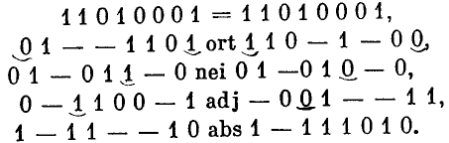Добавление в матрицу U получаемой таким образом новой строки и называется операцией склеивания. Операция поглощения определяется как удаление из матрицы U некоторой строки, поглощаемой какой-либо из других строк этой матрицы. Нетрудно проверить, что данные преобразования матрицы U не изменяют представляемую ею булеву функцию.

По Квайну,  последовательное преобразование ДНФ начинается с совершенной формы, когда ранги всех ее элементарных конъюнкций (определяемые числом букв, образующих конъюнкцию) равны п — числу всех аргументов. Сначала склеиваются все исходные конъюнкции, находящиеся в отношении соседства. После завершения этой операции производятся   всевозможные  поглощения.  Затем склеиваются  все   соседние  конъюнкции

 (n - 1)-го   ранга,  после чего опять выполняются операции поглощения. Так повторяется до тех пор, пока на очередном этапе не окажется, что в преобразуемой ДНФ не существует уже таких конъюнкций, которые находятся в отношении соседства или поглощения. Полученная таким образом ДНФ будет сокращенной. Пусть, например, совершенная ДНФ булевой функции  f  задана матрицей