Кратные, криволинейные и поверхностные интегралы. Векторный анализ (Методические указания к контрольной работе № 8)

Контрольная работа №8

Кратные, криволинейные и поверхностные интегралы.

Векторный анализ.

Литература:  [2], гл.ХIV, ХV; [4], гл.2, 3;

 [5], ч. IV, гл.11 – 13; [12], ч. III.

Основные теоретические сведения

1.  Вычисление площади S  плоской фигуры, ограниченной замкнутой кривой  Г , производится с помощью двойного интеграла по области  D, ограниченной кривой Г, по формуле

,                                                              (1)

если область  D определяется условиями  ,  .

В полярных координатах  ,        формула (1)  принимает вид ,  где   - пределы интегрирования по  являются наименьшим и наибольшим значениями     по области  D.

2.   Объем  V   некоторого пространственного тела   вычисляется с помощью тройного интеграла

.

В свою очередь,  вычисление тройного интеграла сводится к вычислению повторных интегралов:

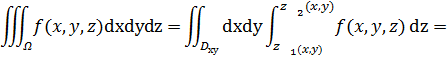
, где  - проекция тела   на плоскость  ,   и   - уравнения поверхностей, ограничивающих область   снизу и сверху соответственно.

3.   Криволинейные интегралы (к.и.) бывают двух типов:

 - к.и.  I -го рода,  Г – кривая;

 - к.и. 2-го рода.

Вычисление К.И. обоих типов сводится к вычислению определенных интегралов. В частности, если кривая Г задается уравнением в прямоугольной системе координат  , , то К.И. 2-го  рода можно записать:

.

Если кривая  Г  задана параметрически  , , , то

.

4.   Вычисление поверхностного интеграла от функции , определенной на двусторонней поверхности  . Сводится к вычислению двойного интеграла, например, вида

,

если поверхность  , заданная уравнением  , однозначно проецируется на плоскость  в область  . Здесь  - угол между единичным вектором нормали   к поверхности   и осью  :

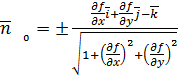,                                                             (2)

т.е. 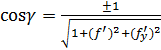, где знак выбирается в зависимости от стороны поверхности .

Векторным полем   называется векторная функция     вместе с областью ее определения. Векторное поле характеризуется скалярной величиной – дивергенцией

и векторной величиной – ротором

.

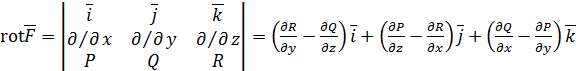Потоком  векторного поля   через поверхность  называется поверхностный интеграл

,

где   - единичный вектор нормали к поверхности          (2).

Формула Остроградского устанавливает связь между потоком векторного поля  через замкнутую поверхность  и дивергенцией поля:

,

где  V  - объем, ограниченный поверхностью .

Циркуляцией векторного поля  по замкнутой кривой  С  называется  к.и. второго рода

,  где

.

Формула Стокса  устанавливает связь между циркуляцией и ротором поля  :

,

где   - поверхность, ограниченная замкнутым контуром  С, а  - единичный вектор нормали к этой поверхности. Направление нормали должно быть согласовано с направлением обхода контура  С.

5.  Векторное поле    называется потенциальным в некоторой области  , если существует такая функция  ,  что

 в обл. .

Функция   называется потенциалом векторного поля  . Очевидно, что потенциал определен с точностью до произвольной постоянной.

Необходимым и достаточным условием потенциальности поля  является выполнение условия в обл. :

.                                                                                   (2)

При выполнении условия (2) потенциал векторного поля может быть найден по формуле

,                          (3)

где   - любой контур, лежащий в обл. , начинающийся в некоторой фиксированной точке  и заканчивающийся в точке , в которой вычисляется потенциал. Интеграл в (3) не зависит от выбора пути интегрирования. Поэтому можно выбирать путь интегрирования удобным для вычислений.

Векторное поле   называется соленоидальным в обл. , если .

Пример 1.     Вычислить криволинейный интеграл  вдоль дуги параболы   от точки  до точки .

Решение.      Из уравнения линии интегрирования находим   . Вычислим криволинейный интеграл, переходя к определенному с переменной интегрирования  у :

.

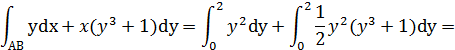
Пример 2.     Вычислить   вдоль дуги С эллипса  , от точки  до точки  .

Решение.      Дуга  С  представляет собой часть эллипса в 1-й четверти. В точке А    ,  в точке  В    .

          .

Пример 3.  С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями .

Решение.  Сделаем чертеж. Поверхности  ;  

- параболические цилиндры. Тело симмет-

 рично относительно координатной плоскости YOZ,  поэтому  вычислим