Численные методы: Методические указания по выполнению практических работ (Вычисление погрешностей результатов арифметических действий. Нахождение экстремумов функции одной переменной приближенными методами)

различается скорость сходимости итерационных процессов по методу Зейделя и методу простой итерации?

2)  Выполните задания 1- 2 для указанного в приложении  номера варианта.

3)Оформите отчет по результатам проделанной работы согласно следующим требованиям:

- в первой части отчета представьте результаты вычислений задания 1;

- во второй части отчета представьте текст расчетной программы с результатами контрольного примера.    

Литература:

• Лапчик М.П. «Элементы численных методов» (стр. 85-108).

Краткие теоретические сведения:

1. Метод простой итерации.

Пусть дана система уравнений вида

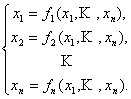(1)

Возьмем некоторое начальное приближение решения                              . Итерационный процесс строится по схеме:

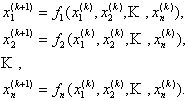(2)

Условие остановки метода  записывается следующим образом:

(3)

Часто величину называют точностью и принимают за погрешность вычислений. Для системы линейных уравнений (1) рекомендуется выбирать

2. Метод Зейделя является модификацией метода простой итерации. Идея данного метода состоит в том, чтобы получаемые в схеме (2) значения сразу же использовались для вычисления следующих          . Схема данного метода будет выглядеть следующим образом:

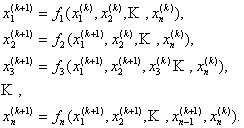
Такой подход позволяет улучшить сходимость итерационного процесса и уменьшить количество итераций, необходимое для достижения заданной точности (3).

Задание1. Найдите вручную первое приближение решения системы уравнений методом простой итерации и методом Зейделя,  определите его абсолютную погрешность и проверьте условия окончания итерационных  процессов.

Пояснение: Система линейных уравнений приведена к виду Х=αХ+β  удобному для вычислений. В качестве начального приближения возьмите  вектор свободных элементов приведенной системы.

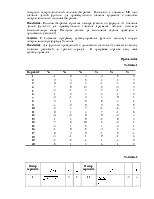
Задание 2. Составьте программу вычисления приближений решения системы методом Зейделя.

Пояснения: Укажите в программе возможности ввода заданной  точности и вывода результатов в таблицу

где Х_1,  Х_2, Х_3, Х₄ – координаты векторов-приближений, Е _k- абсолютная погрешность этих векторов.

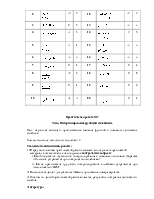
Приложение.

Практическая работа №6

Тема: Интерполирование функции полиномом Логранжа и формулами Ньютона

Цель: Изучить способы построения интерполяционных полиномов; научиться вычислять приближенные значения функций, заданных таблично, различными интерполяционными методами и  программно их реализовывать.

Количество часов, отводимых на работу: 2

Указания по выполнению работы:

1)     Перед выполнением практической работы внимательно изучите теоретический материал, а также ответьте на следующие контрольные вопросы:

1.  В чем состоит задача аппроксимации функций?

2.  В чем состоит особенность аппроксимации таблично заданной функции методом интерполирования?

3.  Как связана степень интерполяционного полинома с количеством узлов при глобальной интерполяции?

4.  В чем заключается идея локальной интерполяции?

5.   В какой форме строится интерполяционный полином Лагранжа?

6.   Как находятся конечные разности различных порядков через значения функции в узловых точках?

7.   Почему первую интерполяционную формулу Ньютона нецелесообразно применять для интерполирования в конце отрезка интерполяции?

2) Выполните задания 1- 4  для указанного в приложении  номера варианта.

3) Оформите отчет по результатам проделанной работы согласно следующим требованиям:

-  в первой части отчета приведите решение задания 1;

- во второй части отчета должны быть представлены таблица конечных разностей данной функции,  результаты субтабулирования функции, к отчету должны быть приложены тексты расчетных программ.

 Литература:

• Лапчик М.П. «Элементы численных методов» (стр. 118-135).

Краткие теоретические сведения:

Определение:Пусть функция f(х) задана таблично на [a,b]:

а=x₀ < x₁ < x₂ < .... < x_n=в ,     y_i = f(x_i) i = 0,...

Тогда построение непрерывной на [a,b] функции F (x) , такой