














Иными словами, годограф
![]() проходит через
проходит через ![]() квадрантов.
квадрантов.
Характеристическое
уравнение разомкнутой системы имеет вид ![]() .
Но так как по условию
.
Но так как по условию ![]() корней лежит в правой
полуплоскости, то в силу критерия Михайлова
корней лежит в правой
полуплоскости, то в силу критерия Михайлова
![]() .
(4.6)
.
(4.6)
Рассмотрим функцию
![]() . (4.7)
. (4.7)
Так как приращение
аргумента годографа ![]() этой функции равно
разности приращения аргумента числителя и знаменателя, то с учетом соотношений
(4.5) и (4.6) получим
этой функции равно
разности приращения аргумента числителя и знаменателя, то с учетом соотношений
(4.5) и (4.6) получим
![]()
![]() .
.
Таким образом, для
устойчивости рассматриваемой системы необходимо и достаточно, чтобы приращение
аргумента годографа ![]() было равно
было равно ![]() . Но функция
. Но функция ![]() связана с передаточной функцией
связана с передаточной функцией ![]() соотношением (4.7). Из этого соотношения
следует, что годограф
соотношением (4.7). Из этого соотношения
следует, что годограф ![]() смещен по отношению к
годографу
смещен по отношению к
годографу ![]() влево на расстояние, равное
влево на расстояние, равное ![]() . Отсюда получаем, что годограф
. Отсюда получаем, что годограф ![]() должен охватывать точку (
должен охватывать точку (![]() ) на угол
) на угол ![]() .
Следовательно, при применении критерия Найквиста необходимо предварительно
определить число правых полюсов
.
Следовательно, при применении критерия Найквиста необходимо предварительно
определить число правых полюсов ![]() .
.
В частном случае, когда
разомкнутая САУ устойчива, т.е. ![]() , критерий
Найквиста состоит в следующем : если разомкнутая САУ устойчива, то для
устойчивости замкнутой САУ необходимо и достаточно, чтобы функция
, критерий
Найквиста состоит в следующем : если разомкнутая САУ устойчива, то для
устойчивости замкнутой САУ необходимо и достаточно, чтобы функция ![]() не охватывала критическую точку (
не охватывала критическую точку (![]() ) при изменении
) при изменении ![]() от
от ![]() до
до
![]() .
.
 |
а)
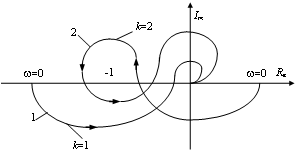 |
б)
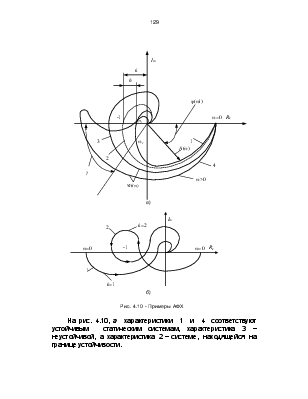
Рис. 4.10 - Примеры АФХ
На рис. 4.10, а характеристики 1 и 4 соответствуют устойчивым статическим системам, характеристика 3 - неустойчивой, а характеристика 2 - системе, находящейся на границе устойчивости.
Существуют
и другие формулировки критерия Найквиста, которые отличаются не сутью, а
формой. Приведем одну из наиболее распространенных в инженерной практике
формулировок : замкнутая САУ устойчива, если число пересечений АФХ ![]() разомкнутой САУ отрицательной
полуоси левее точки (-1, 0) сверху вниз больше на
разомкнутой САУ отрицательной
полуоси левее точки (-1, 0) сверху вниз больше на ![]() раз
числа пересечений в обратном направлении. Здесь
раз
числа пересечений в обратном направлении. Здесь ![]() - по-прежнему число полюсов передаточной функции
- по-прежнему число полюсов передаточной функции ![]() разомкнутой
САУ с положительной действительной частью.
разомкнутой
САУ с положительной действительной частью.
На рис. 4.10, б
в качестве примера показаны две АФХ САУ, неустойчивой в разомкнутом состоянии
из-за наличия правых корней, но устойчивой в замкнутом состоянии.
Характеристика 1 соответствует ![]() (
(![]() , «0,5 пересечения»), характеристика
2 - значению
, «0,5 пересечения»), характеристика
2 - значению ![]() (
(![]() ).
При
).
При ![]() (разомкнутая САУ устойчива или
нейтрально-устойчива) для устойчивости замкнутой САУ разность пересечений
сверху вниз и снизу вверх должна быть равной нулю, т.е.
(разомкнутая САУ устойчива или
нейтрально-устойчива) для устойчивости замкнутой САУ разность пересечений
сверху вниз и снизу вверх должна быть равной нулю, т.е. ![]() .
.
Для одноконтурной САУ,
когда знаменатель ![]() представляет собой
произведение знаменателей передаточных функций отдельных звеньев, число
представляет собой
произведение знаменателей передаточных функций отдельных звеньев, число ![]() находится легко, поскольку
полюсами
находится легко, поскольку
полюсами ![]() являются полюсы передаточных
функций отдельных звеньев. Например, если
являются полюсы передаточных
функций отдельных звеньев. Например, если
![]() ,
, ![]() .
.
Для сложных
многоконтурных САУ, особенно с перекрестными связями, задача определения числа ![]() значительно усложняется (в этих
случаях иногда следует отказаться от критерия Найквиста).
значительно усложняется (в этих
случаях иногда следует отказаться от критерия Найквиста).
Рассмотрим
подробнее систему, находящуюся в разомкнутом состоянии на границе устойчивости.
Для этой системы ![]() , где
, где ![]() - число нулевых корней
характеристического уравнения системы в разомкнутом состоянии.
- число нулевых корней
характеристического уравнения системы в разомкнутом состоянии. ![]() не имеет нулей в правой
полуплоскости и на мнимой оси. Следовательно,
не имеет нулей в правой
полуплоскости и на мнимой оси. Следовательно, ![]() при
при
![]() . По такой характеристике невозможно
судить, охватывает ли
. По такой характеристике невозможно
судить, охватывает ли ![]() точку (
точку (![]() ) или нет (принцип приращения
аргумента также не рассматривает случаи, когда
) или нет (принцип приращения
аргумента также не рассматривает случаи, когда ![]() ).
).
Рис. 4.11 - Сдвиг нулевого корня в левую полуплоскость |
Путем искусственного
сдвига нулевых корней |
Пусть ![]() и
и ![]() ,
тогда
,
тогда
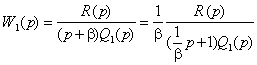 .
.
Разомкнутая система
стала устойчивой. При ![]() оба годографа (
оба годографа (![]() и
и ![]() )
совпадают при всех частотах, кроме
)
совпадают при всех частотах, кроме ![]() отличается от
отличается от ![]() наличием дуги бесконечного
радиуса, проходящей через IV квадрант и приводящей годограф при
наличием дуги бесконечного
радиуса, проходящей через IV квадрант и приводящей годограф при ![]() к действительной положительной
полуоси. Эту часть годографа называют «дополнением в бесконечности».
к действительной положительной
полуоси. Эту часть годографа называют «дополнением в бесконечности».
Годографы АФХ ![]() и
и ![]() рассматриваемой
системы изображены на рис. 4.12.
рассматриваемой
системы изображены на рис. 4.12.
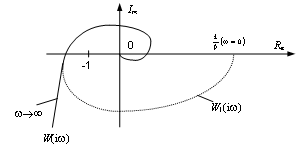 |
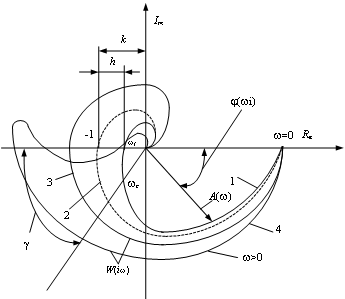
Рис. 4.12 - Дополнение в бесконечности
На рис. 4.12
коэффициент ![]() определяется выражением
определяется выражением ![]() .
.
Аналогично строятся
измененные частотные годографы при ![]() . При
. При ![]() дополнение в бесконечности
проходит через 2 квадранта, а для произвольного
дополнение в бесконечности
проходит через 2 квадранта, а для произвольного ![]() дополнение
в бесконечности представляет собой дугу бесконечного радиуса, начинающуюся при
дополнение
в бесконечности представляет собой дугу бесконечного радиуса, начинающуюся при ![]() на действительной оси и с
увеличением частоты описывающей угол
на действительной оси и с
увеличением частоты описывающей угол ![]() в отрицательном
направлении вокруг начала координат (рис. 4.13).
в отрицательном
направлении вокруг начала координат (рис. 4.13).
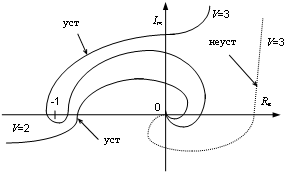 |
Рис. 4.13 - Примеры АФХ астатических САУ
Для АФХ
разомкнутых систем, дополненных в бесконечности, можно воспользоваться
следующей формулировкой критерия Найквиста : для устойчивости замкнутой САУ,
которая в разомкнутом состоянии находится на границе устойчивости, имея нулевые
корни характеристического уравнения, необходимо и достаточно, чтобы АФХ
разомкнутой системы, дополненная в бесконечности, при изменении ![]() от
от ![]() до
до
![]() не охватывала точку (
не охватывала точку (![]() ). Аналогично путем рассмотрения дополнений в бесконечности могут быть
получены условия устойчивости САУ, характеристическое уравнение которой в
разомкнутом состоянии имеет пару мнимых корней. В вычислительном аспекте
алгоритм оценки устойчивости по критерию
). Аналогично путем рассмотрения дополнений в бесконечности могут быть
получены условия устойчивости САУ, характеристическое уравнение которой в
разомкнутом состоянии имеет пару мнимых корней. В вычислительном аспекте
алгоритм оценки устойчивости по критерию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.