Расчёт циклов двигателя внутреннего сгорания. Определение параметров рабочего тела в характерных точках. Расчет положений промежуточных точек по каждому процессу. Расчет основных параметров рабочего тела, страница 2

Процесс 3-4

Изобарный подвод тепла  .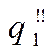

1). Теплоемкость рабочего тела.

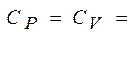
Т. к.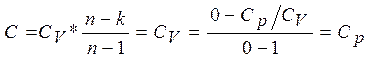

2). Показатель политропы.  n=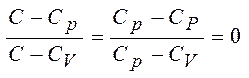

3).Изменение энтальпии.

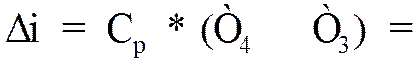
4). Изменение энтропии

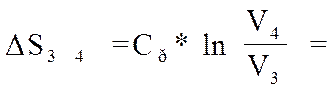
5) Работа процесса.

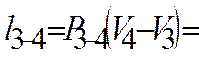
6). Располагаемая работа.

L₀=0. т.к. при изобарном процессе n=0/

7). Подведенное тепло

Сводная таблица по процессу  3-4

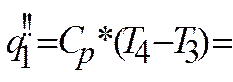
Теплоемкость рабочего тела: С=СV	Показатель политропы n	Изменение энтальпии.	Изменение энтропии	Работа процесса.	Располагаемая работа.	Подведенное тепло

Процесс 4-5.

Адиабатическое расширение.

1). Теплоемкость рабочего тела. q=0,  при  С=0.

2). Показатель политропы  n=k=1,41

3). Изменение энтропии

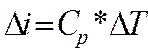= 986,3(Т₅-Т₄)=

 4). Изменение энтропии 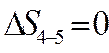, т.к. процесс адиабатный, т. е. dq=0.

5). Работа процесса.

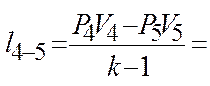
 6). Располагаемая работа

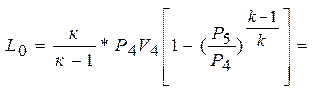
7). Подведенное тепло и отведенное тепло q= 0 (процесс адиабатный).

Сводная таблица по процессу  4-5

Теплоемкость рабочего тела: С=СV	Показатель политропы n	Изменение энтальпии.	Изменение энтропии	Работа процесса.	Располагаемая работа.	Подведенное тепло

Процесс 5-1.

Изохорный подвод тепла q_1.

1). Теплоемкость рабочего тела:   С=С_V=

2). Показатель политропы n=, т. к.   n=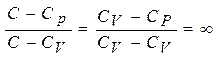

3).Изменение энтальпии.

 

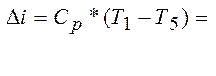
4). Изменение энтропии

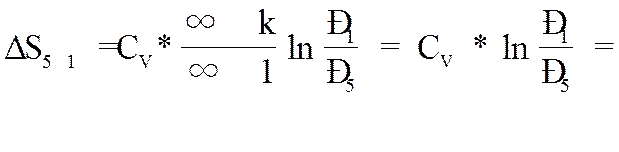
5). Работа процесса.

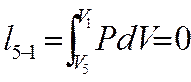, т.к. V= const, значит dV=0.

6). Располагаемая работа.

7). Отведенное тепло

Сводная таблица по процессу  4-5

Теплоемкость рабочего тела: С=СV	Показатель политропы n	Изменение энтальпии.	Изменение энтропии	Работа процесса.	Располагаемая работа.	Подведенное тепло

Теоретический КПД цикла:

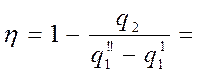
Здесь =+

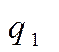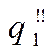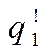
Определим теоретический КПД цикла (через константы):

η =

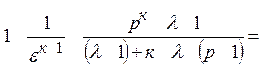
Теоретический КПД цикла Отто (цикл карбюраторного двигателя) с изохорным подводом тепла.

η =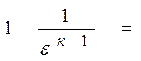

Теоретический КПД цикла Дизеля (цикл компрессорного дизельного двигателя) с изобарным подводом тепла.

Работа цикла

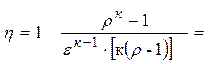
L_ц=(q^!!₁+ q^! ₁)-q ₂=

 

 

Произведём проверку результатов расчёта ΔS:

ΔS₂₃ + ΔS₃₄ = ΔS₅₁

ΔS₅₁ =

следовательно расчёты произведены верно.

Погрешность.

Δ=

Расчет положений точек в масштабе ТS  координатах.

Процесс 2-3

Вычислим положения промежуточных точек в масштабе TS координат. Для удобства построения графика в TS – координатах, составим таблицу положений узловых точек

Таблица 4. Положения узловых точек

	1	2	3	4	5
Т, К
S, кДж/кг·К

ΔS₂₃=∆ S₂₃ = =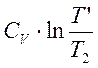              

Сведем  полученные данные в таблицу 5.

Таблица 5. Промежуточные значения (2-3)

Процесс 3-4

∆ S₃₄ = =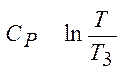

Сведем  полученные данные в таблицу 6

Таблица 6. Промежуточные значения точек    (3-4).                                                                                            

T, K
S, кДж/кг·К

T, K
S, кДж/кг·К

Процесс 5-1

∆ S₅₁ = =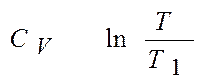

   Таблица 7. Промежуточные значения точек (5-1)                                                                                                                

T, K
S, кДж/кг·К

T, K
S, кДж/кг·К

6. Расчёт сравнения циклов Отто, Дизеля и Тринклера.

Произведём сравнение циклов Отто, Дизеля и Тринклера для двух случаев:

а) когда подводимое тепло и степень сжатия одинаковы;

б) когда двигатели работают при одинаковых условиях (максимальная температура и максимальное давление в цикле одинаковы, начальная температура и давление тоже одинаковы).

а) Подводимое тепло q₁ = const и E = const:

При сравнении этих трех циклов следует учесть, что:

q₁ = q⁰₁ = q^с₁ = q^д₁

цикл Тринклера –	ЦиклОтто:	Цикл  Дизеля.
Мы знаем, что это цикл со смешанным подводом тепла. Значит подводимое тепло: q1 = CV ∙(T3 – T2) + CP∙(T4 – T3) = =	Рассмотрим следующие процессы для различных циклов: q01 = CV ∙(T04 – T2), откуда  T04 = = С учетом условия E = const, вычислим: T05 =   ΔS024 = СV ∙ ln = Выделяемое тепло q02 будет равно: q02 = CV ∙(T1 – T05) =	Процесс 2-40 – изобарное расширение (подвод тепла qД1) q1=Ср=(Т4Д-Т2) Tд4 =   Вычислим Tд5 при E = const Tд5 = T1 ∙ ==      Значит Tд5=1,91,41*263=650,13К Вычислим отводимое тепло qД2 = CV ∙(T1 – TД5) = Дж/кг∙К. ΔSд2-1 = СР ∙ ln
Вычисляем КПД: ηТ =	Вычисляем КПД: η0 =	Ищем КПД: ηд =

Нужно заметить, что q₁ >  q⁰₁ >  q^т₁ >  q^д₁  ;  η⁰ > η^т > η^Д 

Для первого случая имеем η⁰ > η^Т > η^Д  (0,68 > 0,673 > 0,63)

Рассчитаем промежуточные точки процессов:

Процесс 2-4⁰

ΔS = =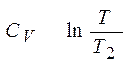

Таблица 8. Промежуточные точки процесса 2-4⁰.