Расчёт идеального цикла двигателя внутреннего сгорания, страница 3

Произведём сравнение циклов Отто, Дизеля и Тринклера для двух случаев:

а) когда подводимое тепло и степень сжатия одинаковы;

б) когда двигатели работают при одинаковых условиях (максимальная температура и максимальное давление в цикле одинаковы, начальная температура и давление тоже одинаковы).

а) Подводимое тепло q₁ = const и E = const:

q₁ = q⁰₁ = q^т₁ = q^д₁

q₁ = C_V ∙(T₃ – T₂) + C_P∙(T₄ – T₃) = 0,699∙(1585 – 834)+0,986∙(2061 – 1585) = 994,28 кДж/кг∙К

q⁰₁ = C_V ∙(T⁰₄ – T₂), откуда T⁰₄ = 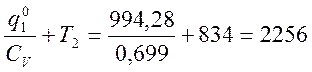К.

T⁰₅ = К.

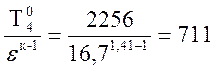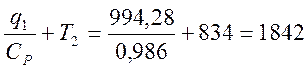T^д₄ = К.

T^д₅ = T₁ ∙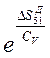

ΔS^д₅₁ = С_Р ∙ ln 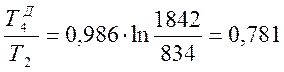кДж/кг∙К.

T^д₅ = 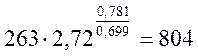К.

ΔS⁰₂₄ = С_V ∙ ln 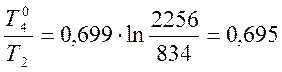кДж/кг∙К.

q⁰₂ = C_V ∙(T₁ – T⁰₅) = 0,699 ∙ (263 – 711) = - 313,15 кДж/кг∙К.

q^Д₂ = C_V ∙(T₁ – T^Д₅) = 0,699 ∙ (263 – 804) = - 378,16 кДж/кг∙К.

η⁰ =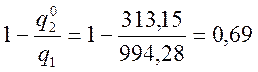

η^д =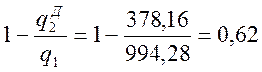

η^Т =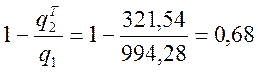

б) Максимальное давление Р₄ = const; температура Т₄ = const, начальное давление Р₁= const, температура Т₁ = const, следовательно q₂ = const и ΔS₄₂ = const.

ΔS⁰₄₂ = С_Р ∙ ln, откуда T⁰₂ = 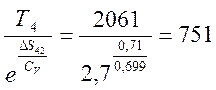К.

Аналогично, ΔS^Д₄₂ = С_V ∙ ln, откуда T^Д₂ = 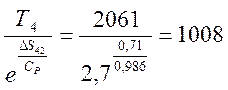К.

q₂ = C_V ∙(T₁ – T₅) = 0,699 ∙ (263 – 834) = - 399,13 кДж/кг∙К.

q^Т₁ = 994,28 кДж/кг∙К. η^Т = 0,68.

q⁰₁ = C_V ∙(T₄ – T⁰₂) = 0,699∙ (2061 – 751) = 915,69 кДж/кг∙К.

q^Д₁ = C_Р ∙(T₄ – T^Д₂) = 0,986∙ (2061 – 1008) = 1038,26 кДж/кг∙К.

η⁰ = 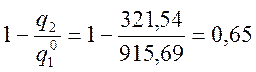η^Д =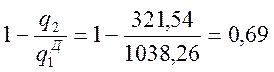

То для первого случая имеем η⁰ > η^Т > η^Д(0,69 > 0,68 > 0,62)

А для второго случая η⁰ < η^Т < η^Д(0,65 < 0,68 < 0,69).

Таблица 9.

	1	2	3	4	5
Р, х 10⁵ Па	1,0	53,15	101	101	2,75
V, м³/кг	0,754	0,045	0,045	0,059	0,754
Т, К	263	834	1585	2061	723

Таблица 10.

	l, кДж/кг	Δ i, кДж/кг	ΔS,кДж/кгК	q, кДж/кг	C, кДж/кг	n
1 – 2	-399,45	563	0	0	0	1,41
2 – 3	0	740,49	0,45	524,95	0,699	∞
3 – 4	469,34	469,34	0,26	469,34	0,986	0
4 – 5	947,68	-1319,27	0	0	0	1,41
5 – 1	0	-453,56	0,71	-321,54	0,699	∞

Таблица 11.

	q₁,кДж/кг	q₂,кДж/кг	η	q₁,кДж/кг	q₂,кДж/кг	η
Цикл Отто	994,28	-313,15	0,69	881,44	-321,54	0,65
Цикл Дизеля	994,28	-378,16	0,62	991,92	-321,54	0,69
Цикл Тринклера	994,28	-321,54	0,68	937,81	-321,54	0,68

Найдём положения промежуточных точек сравнительных процессов в масштабе ТS – координат.

а) ΔS = C_V∙ln

Таблица 12.

Отто/Т, К	1000	1240	1480	1720	1960	2200
S, кДж/кг∙К	0,127	0,277	0,401	0,506	0,597	0,678

ΔS = C_Р∙ln

Таблица 13.

Дизель/Т,К	950	1120	1290	1460	1630	1800
S, кДж/кг∙К	0,128	0,291	0,430	0,552	0,661	0,758

б) ΔS = C_V∙ln

Таблица 14.

Отто/Т,К	950	1150	1350	1550	1750	1950
S, кДж/кг∙К	0,164	0,299	0,410	0,506	0,591	0,667

ΔS = C_Р∙ln

Таблица 15.

Дизель/Т,К	1150	1320	1490	1660	1830	1950
S, кДж/кг∙К	0,130	0,266	0,385	0,492	0,588	0,651

7. Заключение.

Вывод: Данный цикл ДВС, расчёт которого мы провели, считается идеальным, потому что рабочим телом считается воздух с постоянной теплоёмкостью (μ = 29 Дж/моль∙К, C_V = 0,699 кДж/кг∙К , C_Р = 0,986 кДж/кг∙К); химический процесс горения топлива заменяется подводом тепла q₁; выпуск отработавших газов – процессом отвода тепла q₂, механические и тепловые потери почти отсутствуют. Провели сравнение циклов работы двигателей Отто, Дизеля и Тринклера в двух случаях: 1) когда q₁ = const и ε = const; 2) когда двигатели работают при одинаковых условиях (Р₄ = const, T₄ = const, T₁=const, P₁= const). Наибольший КПД имеет цикл Отто в 1-ом случае (η⁰ = 0,69), а во 2-ом случае цикл Дизеля (η^Д = 0,69).

8.Список использованной литературы:

1. Алексеев Г.Н. Общая теплотехника: Учеб. пособие. – М.: Высш. Школа, 1980. – 552 с., ил.

2. Нащёкин В.В. Техническая термодинамика и теплопредача. М.: Высшая школа, 1975.

3. Теплотехника. Под ред. Баскакова А.П. М.: Энергоиздат, 1991.

4. Лопарев А.В., Болотов А.К. Сборник задач по теплотехнике. М.: Киров, 2001.

1 2 3

Скачать файл