Определение расхода воздуха через экспериментальную установку. Расчет распределений скоростей и давлений в объеме циклонной камеры

Результаты расчетов  для остальных опытов приводим в виде таблицы 3.

Таблица 3. Результаты обработки опытных данных по конвективному теплообмену

Номер опыта	1	2	3	4	5
Площадь поверхности теплообмена калориметра (Fц, м2)	0,049761	0,049761	0,049761	0,049761	0,049761
Площадь боковой поверхности циклонной камеры (Fст, м2)	0,342800	0,342800	0,342800	0,342800	0,342800
Суммарный тепловой поток от калориметра к охлаждаю-щему воздуху (Q, Вт)	368,129	341,1834	280,1416	227,3904	214,3136
Температуры насыщения (tн, °C)	101,1128	101,1161	101,1295	101,2803	101,3071
Теплота парообразования (rп, Дж/кг)	2253698	2253689	2253653	2253249	2253177
Лучистый тепловой поток между калориметром и боковой поверхностью циклонной камеры (Qл, Вт)	7,178261	7,19350	7,219673	7,276074	7,293741
Конвективный тепловой поток (Qк, Вт)	360,9507	333,98994	272,9219	220,1143	207,0198
Приращение температуры воздуха, охлаждающего кало-риметр (t, С)	4,879519	5,034134	5,342604	5,359097	5,940205
Средняя температура циклонного потока (tср,С)	12,63976	12,41707	12,0713	11,27955	11,2701
Коэффициент теплоотдачи конвекцией от калориметра к закрученному воздуху (aк, Вт/(C*м^2))	83,6574	77,33642	63,24391	50,79737	47,85683
Число Нуссельта (Nu)	148,6578	137,5235	112,5882	90,6605	85,415
Коэффициент теплопроводности воздуха при средней температуре потока (lср, Вт/(м*С))	0,025324	0,025306	0,025214	0,025214	0,025213
Плотность воздуха на радиусе rm (rm, м^2/C)	1,277971	1,274943	1,26564	1,26564	1,262666
Коэффициент кинематической вязкости воздуха на ра-диусе rm(nm, м^2/с)	1,39E-05	1,39E-05	1,40E-05	1,40E-05	1,40E-05
Число Рейнольдса (Re m)	1,64E+05	1,55E+05	1,14E+05	9,30E+04	7,54E+04

После обработки опытных данных по теплоотдаче для всех режимов по числу Рейноль-дса  устанавливается функциональная связь между числами Nu и Rе_jm в виде зависимости:

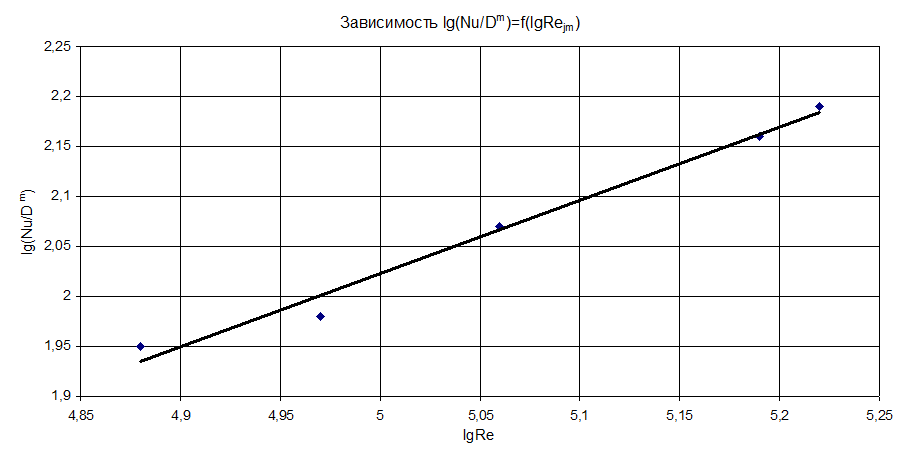
            Для нахождения коэффициентов А и n в уравнении подобия результаты опытов представляют графически как функцию  

Применим метод наименьших квадратов для окончательной обработки результатов экспериментов. Запишем зависимость в виде:

где .

Применительно к рассматриваемой задачи расчетные соотношения для коэффициентов n,A имеют вид:

n=;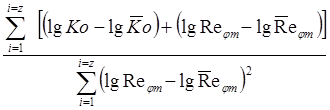                                  

A= antilg(lg Ko- n lgRe)² где                                                              

Для удобства вычислений  результаты прoмежуточных расчетов  заносим в таблицу 4.

Таблица 4.Статическая обработка опытных данных

Номер опыта	1	2	3	4	5
lgKo	2,19	2,16	2,07	1,98	1,95	10,35
(lgKo)2	4,7961	4,6656	4,2849	3,9204	3,8025	21,4695
lgRejm	5,22	5,19	5,06	4,97	4,88	25,32
(lgRejm)2	27,2484	26,9361	25,6036	24,7009	23,8144	128,3034
lgKo×lgRejm	11,4318	11,2104	10,4742	9,8406	9,516	52,473
lgKo-lgKo	0,12	0,09	0	-0,09	-0,12	6,66E-16
lgRejm- lgRejm	0,156	0,126	-0,004	-0,094	-0,184	-8,9E-16
(lgKo-lgKo)´ (lgRejm- lgRejm)	0,01872	0,01134	0	0,00846	0,02208	0,0606
(lgKo-lgKo)2	0,0144	0,0081	0	0,0081	0,0144	0,045
(lgRejm- lgRejm)2	0,024336	0,015876	0,000016	0,008836	0,033856	0,08292

;                        

Тогда  подставляя эти значения в формулы для n,A получим n=0,7308, A=0,0234 и окончательное уравнение, описывающие данный процесс следующие: 

5.  Расчет статистических показателей

Общая дисперсия (рассеивание) точек относительно среднеарифметического значения lgKo для опытов определяется по уравнению:

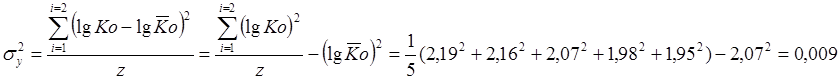            Дисперсия точек относительно линии регрессии находится следующим образом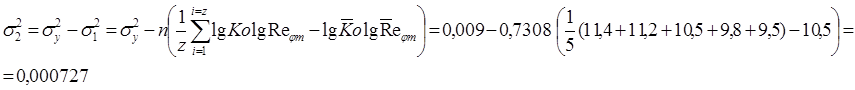                            

где  - дисперсия относительно среднего значения lgKo.            

Величину среднеквадратичного отклонения экспериментальных точек от прямой линии регрессии, называемую иначе стандартом отклонения:

Границы доверительного интервала по Ко оцениваются уравнением

, где t  -   коэффициент Стьюдента, определяемый в зависимости от величины выборки (числа опытов);

Относительная величина отклонения опытных точек от расчётной зависимости                                  .

Характеристикой тесноты и достоверности связи между величинами Ко и Re_jm  является коэффициент корреляции

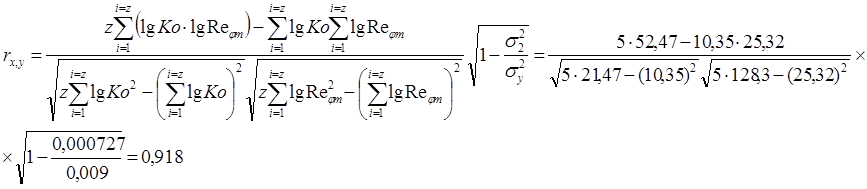
Оценка достоверности прямолинейной связи производится исходя из необходимости выполнения условия:

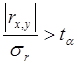
где  s_r - среднеквадратичная погрешность коэффициента корреляции, вычисляемая по прибли-женной зависимости:

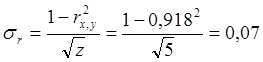
Тогда 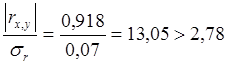  , значит условие выполняется.

6. Расчет погрешностей измерений

Предельная относительная погрешность измерения расхода равна:

где s_q – средняя квадратичная погрешность измерения расхода, которпя определяется по формуле:

где s_a, s_e, s_Dр, s_r - среднеквадратичные относительные погрешности соотвественно расхода, поправочного множителя на расширение среды, измерения перепада давления дифференциальным микроманометром, плотности измеряемой среды.

Средняя квадратичная относительная погрешность коэффициента расхода для диафрагм рассчитывается по уравнению:

где s_aи, s_к1, s_к2, s_к3 – среднеквадратичные относительные погрешности соответственно исходного коэффициента расхода, а также поправочных коэффициетов к₁, к₂, к₃

Среднеквадратичная относительная погрешность поправочного множителя на расширение измеряемой среды e определяется по формуле:

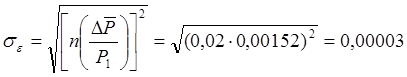
где n – множитель, принимаемый равным 0,02

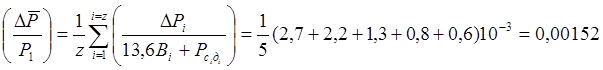- среднеарифметическая величина перепада давления на диафрагме