Применение приложений Microsoft Office для курсового проектирования

Анализ результатов вычислений и их графическая интерпретация.

ВВЕДЕНИЕ

Одним из перспективных и эффективных путей разрешения проблемы интенсификации процессов тепломассообмена в теплоэнергетических и теплоиспользующих установках и устройствах является применение закрученных высокотурбулентных потоков жидкостей и газов. Вращающиеся течения уже широко используются при организации сжигания топлива в вихревых горелках, циклонных топках и камерах сгорания, проведении процессов нагрева и термообработки в циклонно-вихревых нагревательных устройствах, сушки материалов в рециркуляционных сушилках и т. п.

Изучение гидродинамики и теплообмена в циклонно-вихревых камерах представляет собой важную практическую задачу (12-17), так как позволяет получить необходимые данные для их расчета и проектирования. Интересна в этом плане задача исследования теплоотдачи круглого цилиндра, соосного с аэродинамической осью стабилизированного циклонного потока, с точки зрения дальнейшего изучения особенностей теплообмена в поле центробежных сил, а также разработки рекомендаций по расчету конвективного теплообмена в вихревых МГД (магнитогидродинамических) генераторах, циклонных печах, при вихревом охлаждении элементов электрических машин, полупроводниковых выпрямителей и т.п. (8, 9, 18, 20).

ЗАДАЧИ И ЦЕЛЬ РАБОТЫ

Цель работы – привить студентам определенные навыки выполнения самостоятельных научных исследований в области конвективного теплообмена. Непосредственно выполнению работы предшествует изучение специальной научной и рекомендуемой учебной литературы, методики проведения опытов и обработки результатов исследования.

В работе осуществляется экспериментальное изучение теплоотдачи конвекцией от вертикального цилиндра к закрученному потоку воздуха в циклонной камере, обработка и анализ результатов наблюдений, составление уравнения подобия для расчета конвективного теплообмена, расчет статистических показателей, характеризующих отклонение опытных точек от рекомендуемой расчетной зависимости, оценка степени достоверности результатов и погрешностей измерений.

В заключительной стадии работы составляется пояснительная записка с внесением в нее всех опытных и расчетных материалов и оформлением графической части.

1.  ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ

Сложная аэродинамическая структура потока в циклонных камерах в значительной степени ограничивает возможности использования математических методов решения задачи конвективного теплообмена, поэтому основным направлением в изучении теплоотдачи конвекцией является эксперимент.

Особенность рассматриваемой задачи конвективного теплообмена в закрученном циклонном потоке заключается в том, что при движении среды возникают инерционные массовые (центростремительные) силы, которые практически полностью определяют условия теплоотдачи.

Анализ системы дифференциальных уравнений движения и теплообмена применительно к рассматриваемой задаче (17), а также использование рекомендаций работы В.К.Щукина (21) показывают, что особенности теплоотдачи цилиндра в закрученном потоке определяются главным образом массовыми (центростремительными) силами, а задача определения коэффициентов теплоотдачи фактически сводится к установлению зависимости

Nu=f(P,Pr),                                                                            (1)    где Nu=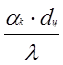- число Нуссельта;

(a_к- коэффициент теплоотдачи конвекцией от цилиндра к закрученному потоку; d_ц- внешний диаметр цилиндра; l- коэффициент теплопроводности среды);

P= - критерий, определяющий движение жидкости и теплоотдачу в закрученном потоке (j_m- максимальное значение центростремительного ускорения j в системе; l_m- характерный линейный размер, определяющий положение j_m относительно поверхности теплоотдачи; DТ- разность температур в точках потока, где инерционное ускорение достигает максимального и минимального значений; b,n -коэффициенты объемного расширения и кинематической вязкости среды; P_r=n/a - критерий Прандтля,                 а- коэффициент температуропроводности).

В рассматриваемой задаче минимальное ускорение имеет место на поверхности теплоотдачи (цилиндра) и равно нулю. Физические константы в уравнении (1) определяются по средней температуре потока, практически равной температуре в точке потока, где j=j_m.

При сравнительно небольших температурных напорах DТ (в условиях, близких к изотермическим) сомножитель (1+bDТ) незначительно отличается от единицы, а при небольших изменениях DТ, даже если и отличается от единицы, то изменяется сравнительно мало. Поэтому изменение критерия P полностью определяется безразмерным комплексом (21).

S=                                                                                        (2)

В рассматриваемой учебной работе исследование теплоотдачи выполняется в воздушном потоке в узком интервале его температуры и только при одном направлении теплового потока, поэтому из искомого уравнения подобия (1) может быть исключен критерий Прандтля и температурный фактор (17).

S(1+bDT)=S_изот

Условие подобия процессов конвективного теплообмена в поле центростремительных сил в изотермической и неизотермической системах предполагает существование равенства (21).

Поэтому для того, чтобы критерий S в неизотермических условиях отражал влияние центростремительных сил на явление с учетом неизотермичности потока, он должен определяться в общем виде по формуле

S=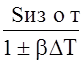                                                                                     (3)

Знак плюс (+) соответствует нагреву среды; знак минус (-) –охлаждению (21).

Таким образом, для описания процесса конвективного теплообмена в рассматриваемой задаче может быть использовано уравнение

Nu=f(S)                                              (4)

Анализ критерия S с использованием результатов исследований аэродинамики циклонных камер и созданной на их основе методики аэродинамического расчета (5,16,19) позволил установить, что он может быть заменен на число Рейнольдса Rl_jm, рассчитанное по максимальной вращательной скорости в рабочем объеме циклонной камеры w_jm. Эта связь определяется уравнением

S=Rl²_jm                                                                                     (5)

Здесь Rl_jm=, где n_m - коэффициент кинематической вязкости среды в точке, где вращательная скорость равна максимальной; D=D(h_я,b)– безразмерный комплекс, зависящий от аэродинамических характеристик потока;

h_я= -безразмерный радиус осесимметричного ядра потока (r_я- радиус  ядра  потока;  r_ц  -  радиус  цилиндра; r_jm  -  радиус, определяющий положение w_jm);

b=-безразмерный параметр.

Величины r_я,b зависят от основных геометрических параметров циклонной камеры и могут быть рассчитаны по методике, изложенной в работе (16), либо определены по экспериментально найденному профилю вращательной скорости в объеме камеры. Значения D в зависимости от r_я,b приведены в табл.1.

Таблица 1.            Значения комплекса D=D(h_я,b) при h_я.

Замена S на Rl_jm дает определенные преимущества в обработке опытных