Дополнительные расходы, связанные с проведением селекции или сортировки элементов схемы должны окупаться за счет экономии, получаемой при изготовлении электрорадиоэлементов с более широкими допусками.
Вместе с тем следует иметь в виду, что экономическая целесообразность использования метода групповой взаимозаменяемости значительно уменьшается при увеличении количества элементов, проходящих селекцию или сортировку и, за счет наличия незавершенного производства (т.е. остатков электрорадиоэлементов не вошедших в комплекты для сборки).
Метод подгонки. Сущность метода состоит в том, что требуемая точность выходных контролируемых параметров изготавливаемых узлов достигается подбором одного или нескольких схемных элементов с постоянными параметрами, применение которого в схеме узла обеспечивает частичную или полную компенсацию погрешностей выходных контролируемых параметров.
Подбираемый элемент называется компенсатором. В качестве компенсаторов рекомендуется выбирать элементы, с наибольшей чувствительностью, чтобы уменьшить количество значений подбираемых параметров.
Метод регулировки обеспечивает точность выходных контролируемых параметров изготавливаемых узлов путем изменения первичного регулируемого параметра компенсирующего элемента, в качестве которого применяют специальные схемные элементы с переменными параметрами - регулировочные элементы.
Метод регулировки аналогичен методу подгонки. Однако в случае раскомпенсации имеется возможность ее восстановления. Регулировочный элемент с переменным параметром позволяет получить необходимую точность не только при изготовлении, но и в период эксплуатации. Он компенсирует производственные погрешности и погрешности, являющиеся следствием изменения температуры и старения схемных элементов.
Наряду с достоинствами метод регулировки имеет недостатки: регулировочный элемент, поставленный в схему, снижает надежность аппаратуры, так как надежность регулировочных элементов значительно ниже надежности элементов с постоянными параметрами; кроме того наличие регулировочных элементов в схеме значительно усложняет технологический процесс изготовления аппаратуры.
2. Анализ методов сборки делителя напряжения
Схема делителя напряжения представлена на рис. 1. Основным выходным параметром делителя является коэффициент передачи (коэффициент деления) по напряжению
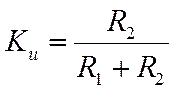 .
(5)
.
(5)
При этом ![]() . Уравнение погрешности выходного
контролируемого параметра
. Уравнение погрешности выходного
контролируемого параметра ![]() может быть
записано следующим образом:
может быть
записано следующим образом:
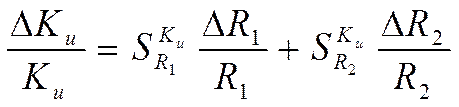 ,
,
где 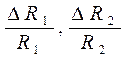 - относительные
погрешности сопротивлений резисторов
- относительные
погрешности сопротивлений резисторов ![]() ,
, ![]() ;
; 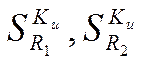 -
чувствительности (коэффициенты влияния) выходного параметра
-
чувствительности (коэффициенты влияния) выходного параметра ![]() к вариациям первичных параметров сопротивлений
резисторов
к вариациям первичных параметров сопротивлений
резисторов ![]() ,
, ![]() .
.
Чувствительности 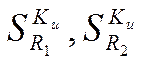 ,
используя выражение (5), определяются следующим образом:
,
используя выражение (5), определяются следующим образом:
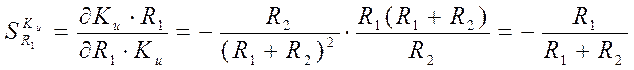 ;
;
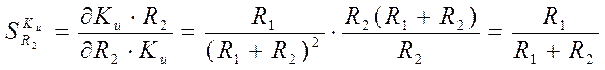 .
.
При ![]() ,
, ![]() =
=![]() и
и ![]() ;
; ![]() .
Тогда уравнение погрешности запишется следующим образом
.
Тогда уравнение погрешности запишется следующим образом
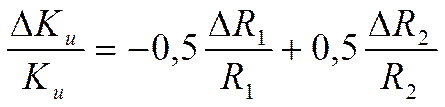 .
.
Сделаем следующие допущения.
1. Закон распределения погрешностей схемных параметров – нормальный.
2.
Погрешности схемных параметров ![]() и
и ![]() не
кореллированы
не
кореллированы
3. Центр группирования совпадает с серединой поля допуска.
4. В поле допуска находится 99,73% всех случайных отклонений.
Тогда можно записать, что ![]() ,
так как
,
так как ![]() =
= ![]() .
.
Уравнение допусков при статистическом методе расчета с полной взаимозаменяемостью в данном случае запишется следующим образом:
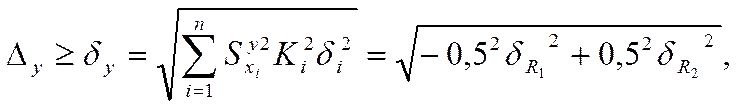
полагая ![]() =10% и
=10% и 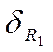 =
=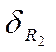 =
=![]() , уравнение допусков перепишется в
виде
, уравнение допусков перепишется в
виде
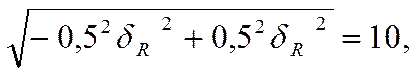 или
или 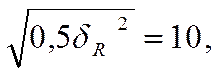
тогда 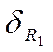 =
=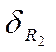 =
=![]() =
= 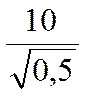 =14,3%.
=14,3%.
Расчет допусков по методу максимума-минимума в тех же условиях сводится к следующему
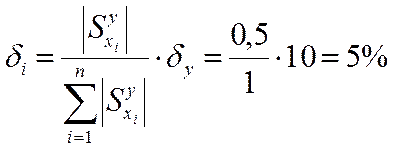 , причем полная
взаимозаменяемость будет выполняться независимо от вида законов распределения
погрешностей.
, причем полная
взаимозаменяемость будет выполняться независимо от вида законов распределения
погрешностей.
Из сравнения приведенных расчетов видим, что допуски рассчитанные по статистическому методу почти в три раза шире допусков, рассчитанных по методу максимума-минимума.
Рассмотрим расчет допусков на параметры
сопротивлений резисторов делителя по методу неполной взаимозаменяемости.
Допустим, что процент риска равен 5% , тогда коэффициент относительного
рассеяния ![]() = 1,33. Уравнение допусков в данном
случае запишется следующим образом:
= 1,33. Уравнение допусков в данном
случае запишется следующим образом:
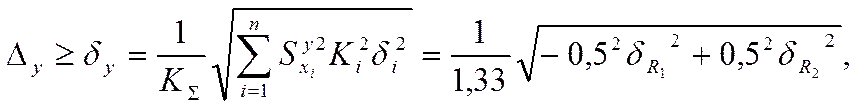
аналогично полагая ![]() =10%
и
=10%
и 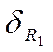 =
=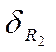 =
=![]() , уравнение допусков перепишется в
виде
, уравнение допусков перепишется в
виде
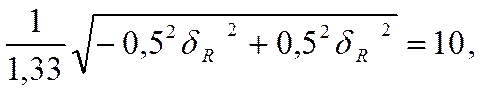 или
или 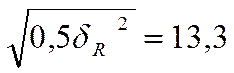 ,
,
тогда 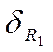 =
=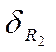 =
=![]() =
= 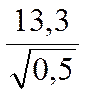 = 19%.
= 19%.
При расчете допусков на параметры сопротивлений резисторов для сборки с групповой взаимозаменяемостью воспользуемся методом максимума-минимума, так как законы распределения погрешностей в группах рассортированных деталей неизвестны. Тогда
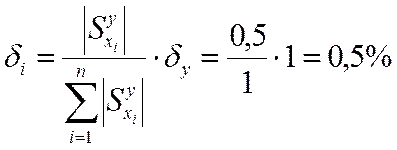 , а величина
поля группового допуска равна
, а величина
поля группового допуска равна 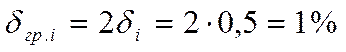 .
.
Таким образом партия
резисторов рассортировывается на группы шириной 1%, поскольку![]() , то комплекты для сборки делителей
формируются из пар резисторов принадлежащих к одной группе. Для проверки
погрешностей выходного параметра воспользуемся уравнением погрешности (1). Для
группы с границами [9,10]% наихудший случай сборки
, то комплекты для сборки делителей
формируются из пар резисторов принадлежащих к одной группе. Для проверки
погрешностей выходного параметра воспользуемся уравнением погрешности (1). Для
группы с границами [9,10]% наихудший случай сборки
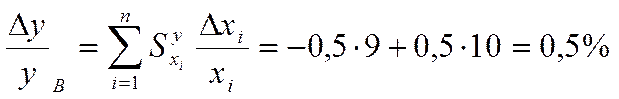 ,
,
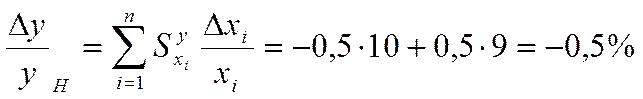 .
.
С учетом взаимной компенсации идентичных погрешностей ширину групп
сортировки можно увеличить в 2 раза, т.е. 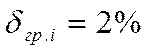 .
.
ЛИТЕРАТУРА
1. Гусев В.П. Технология радиоаппаратостроения. Учебное пособие для вузов. М.: Высшая школа. 1972. 496с.
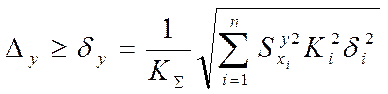
При cборке по методу полной взаимозаменяемости любая сборочная
единица (деталь, элемент),
выполненная в пределах заданных допусков, входит в сборочный комплект. Случай двух параметров ![]() и
и
![]() , образующих
сборочный комплект у, представлен
на рис. 1. Таким образом, осуществляется
так называемая сплошная сборка, при которой исходные, годные детали полностью
взаимозаменяемы. Сборка, основанная на полной взаимозаменяемости, обеспечивает
наиболее простую технологию сборочного
процесса по сравнению с другими методами. Однако в ряде случаев, при высоких
требованиях к точности выходных параметров yдопуски на первичные
параметры
, образующих
сборочный комплект у, представлен
на рис. 1. Таким образом, осуществляется
так называемая сплошная сборка, при которой исходные, годные детали полностью
взаимозаменяемы. Сборка, основанная на полной взаимозаменяемости, обеспечивает
наиболее простую технологию сборочного
процесса по сравнению с другими методами. Однако в ряде случаев, при высоких
требованиях к точности выходных параметров yдопуски на первичные
параметры ![]() могут быть настолько малы, что будут
экономически нецелесообразными.
могут быть настолько малы, что будут
экономически нецелесообразными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.