Электромагнитные явления. Постоянный ток и магнитное поле. Электромагнитная индукция. Энергия магнитного поля (Контрольные задания по физике)

Потенциал в какой-либо точке электрического поля 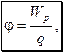  где W_р – потенциальная энергия заряда q, помещённого в данную точку.

Для точечного заряда q на расстоянии r от него величина напряжённости 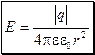;             потенциал  .

Принцип суперпозиции. Напряжённость поля нескольких зарядов равна векторной сумме напряженностей отдельных зарядов:

, где ;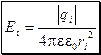

r_i – расстояние от заряда q_i  до точки, в которой определяется напряжённость;  i – номер заряда; п – число зарядов, создающих поле. Потенциал поля нескольких зарядов равен алгебраической сумме потенциалов отдельных зарядов:

, где .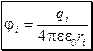

 Поток вектора напряжённости электростатического поля равен произведению вектора напряжённости на площадь S поверхности, сквозь которую проходят силовые линии, с учётом угла a между вектором напряжённости и нормалью к поверхности:

.

Теорема Остроградского–Гаусса: поток вектора напряжённости электростатического поля сквозь любую замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой замкнутой поверхностью, делённой на e₀e:

.

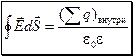Напряжённость электрического поля:

·  равномерно заряженной плоскости ;

·  равномерно заряженной нити  на расстоянии r от неё .

Здесь    – поверхностная плотность заряда на плоскости;  – линейная плотность зарядов на нити; e – диэлектрическая проницаемость окружающей среды.

Работа, совершаемая при перемещении заряда q в электрическом поле

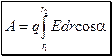.В однородном поле  A = qElcosa , где l — величина перемещения; a — угол между направлениями векторов напряженности электрического поля и перемещения.

Работа, совершаемая электростатическим полем при перемещении заряда q из точки поля с потенциалом j₁в точку с потенциалом j₂,  

 A = q(j₁ – j₂) .

Напряжённость электрического поля и потенциал связаны соотношением

В случае однородного поля – например, в  плоском конденсаторе

где j₁ – j₂ — разность потенциалов между пластинами конденсатора; d – расстояние между ними.

Потенциал j уединенного проводника и его заряд q связаны соотношением

 q = Cj  ,  где C – ёмкость проводника.

Ёмкость:

– плоского конденсатора 

 C = e₀ e S/d ,  где S — площадь каждой пластины конденсатора.

– уединенного шара  

 C = 4pe₀ eR ,  где R — радиус шара.

Ёмкость системы конденсаторов:

- при параллельном соединении                  

 С = С₁ + С₂ + С₃ + ...,

– при последовательном соединении           

 .

Энергия заряженного конденсатора 

Объемная плотность энергии электрического поля 

.

Постоянный ток

Сила тока I равна количеству электричества, проходящему через поперечное сечение проводника в единицу времени:

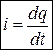. Если I = const, то

Плотность электрического тока

, где S — площадь поперечного сечения проводника.

Закон Ома для участка цепи:

, где U — разность потенциалов на концах участка и R — сопротивление данного участка.

Для замкнутой цепи закон имеет вид

где e — эдс источника тока; R — внешнее сопротивление; r — внутреннее сопротивление источника тока.

Сопротивление проводника , где r — удельное сопротивление материала;

l и S — длина проводника и площадь его поперечного сечения.

Работа и мощность электрического тока:  

          

Коэффициент полезного действия источника тока  .

Магнитное поле

В соответствии с законом Био — Савара — Лапласа элемент контура dl, по которому течет ток I, создает в некоторой точке А магнитное поле напряженностью

где r — расстояние от dl до точки А, a — угол между радиус-вектором r и элементом dl.

Напряженность магнитного поля:

– в центре кругового тока

 где R — радиус кругового контура с током.

– бесконечно длинного проводника с током на расстоянии a  от него

– внутри тороида  и бесконечно длинного соленоида

 H = In,   где n — число витков на единицу длины.

Магнитная индукция В связана с напряженностью Н магнитного поля соотношением

 В = m₀ m Н , где m₀ — магнитная постоянная (m₀ = 4p×10^–7 Гн/м);  m — магнитная проницаемость среды.

Поток магнитной индукции сквозь контур

 Ф = BS cosj , где S — площадь контура; j — угол между нормалью к плоскости контура и направлением магнитного поля.

На элемент dl проводника с током, находящийся в магнитном поле, действует сила Ампера

dF = BI sinadl  ,

где a — угол между направлениями тока и магнитного поля. Направление силы определяется по правилу левой руки.

Сила Лоренца, действующая на заряженную частицу, движущуюся со скоростью u в магнитном  поле,  определяется  формулой:

 F = quB sina , где q — заряд частицы и a — угол между направлениями скорости частицы и магнитного поля. Направление силы Лоренца всегда перпендикулярно скорости частицы