Лабораторная работа ФЦ–2
Изучение дифракции света и определение длины световой волны
Цель работы: изучить явление дифракции света, определить период дифракционной решётки и длины световых волн основных цветов.
Оборудование: оптическая скамья, источник света – лампа накаливания, линейка со щелью, дифракционная решётка, лазер.
Краткая теория
Белый свет, например, солнечный, состоит из непрерывного набора длин волн в диапазоне от 400 до 760 нм. Для определения длины волны нужно разложить белый свет в спектр. Это легко сделать с помощью дифракционной решётки, работающей на явлении дифракции света — отклонения лучей (волны) от прямолинейного пути при встрече с препятствием, размеры которого не сильно отличаются от длины волны. Волны, отклонённые препятствием, когерентны, и, следовательно, при их наложении будет наблюдаться интерференция света – чередование светлых и тёмных полос разного цвета
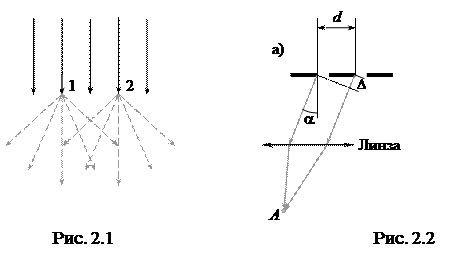 |
На рис. 2.2 показаны те лучи от вторичных источников, которые отклонились от прямой на угол a. Эти лучи проходят сквозь две соседние щели дифракционной решётки, В точке А экрана они дадут интерференцию, то есть там будет наблюдаться максимум для длины волны l, если разность хода этих волн равна целому числу длин волн:
|
D = kl , |
(1) |
где k = 0, ±1, ±2, ±3, … — целое число, называемое порядком интерференции.
Как следует из рис. 2.2, разность хода Dможно выразить через период d дифракционной решётки (эту величину называют также постоянной дифракционной решётки) — расстояние, равное суммарной ширине прозрачной и темной полоски (см. рис. 2.2):
|
D = d sin a. |
(2) |
Ширина прозрачных и непрозрачных полос должна быть соразмерна длине волны, иначе дифракция наблюдаться не будет. Это условие очевидно: при d >> l синус угла a и, следовательно, угол a в (2) будут стремиться к нулю, и дифракционные максимумы и минимумы будут накладываться друг на друга, создавая равномерную освещённость вместо полосатой картины. Из выражений (1) и (2) легко получить условие главных дифракционных максимумов — формулу дифракционной решётки
|
d sin ak = kl ; (k = 0, ±1, ±2, ±3, …). |
(3) |
Из этого равенства следует, что угол отклонения всех максимумов (кроме нулевого) зависит от длины волны: чем больше l, тем на больший угол отклоняется волна. Поскольку волны разной длины (а, значит, и разного цвета!) отклоняются на разные углы, то белый свет в максимумах 1-го, 2-го и более высоких порядков разлагается в сплошной спектр. Максимум нулевого порядка будет белым, потому что при k = 0 условие максимумов выполняется для всех длин волн.
Равенство (3) может быть использовано для экспериментального определения длины волны. Для этого нужно: 1) добиться, чтобы падающие на решётку лучи были достаточно когерентными; 2) определить среднее значение sin a для максимума соответствующего цвета.
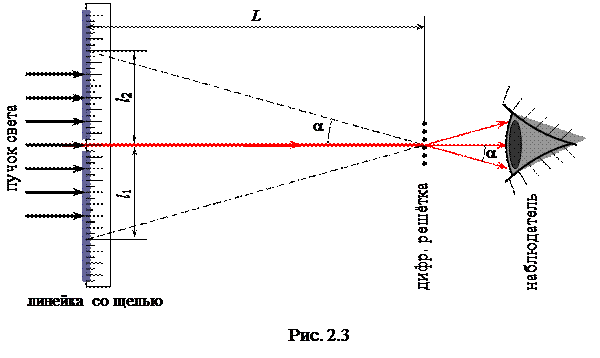
Выполнение первого условия достигается
тем, что свет пропускается сквозь узкую щель (рис. 2.3).
Синус угла отклонения (см. рис. 2.3) равен отношению противолежащего катета к гипотенузе:
|
|
(4) |
При малых углах (<10°) sin a. » tg a, и расчётная формула для определения длины волны упрощается:
|
|
(5) |
Здесь < l > — среднее значение отклонений l1и l2 для соответствующего цвета.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.