Пневматическая тормозная система троллейбуса (Исследовательская часть проекта (исследование динамики контура))

5. Исследовательская часть проекта (исследование динамики контура)

Целью динамического расчета является выбор параметров гидропривода, которые обеспечивают заданное быстродействие при минимальном перерегулировании. По результатам расчета строятся характеристики привода. Для получения математической модели составляется расчетная схема, и принимается ряд допущений при переходе от реального привода к расчетной схеме. От вида и количества принятых допущений будет зависеть сложность и адекватность модели.

Составим математическую модель для контура цилиндра перемещения рабочего стола с распределителем на входе и с учетом сжимаемости жидкости. Расчетная схема представлена на рисунке 5.1.

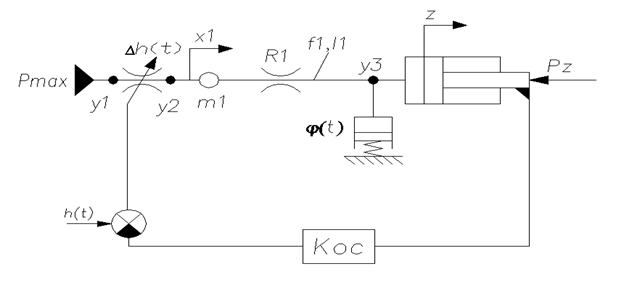
Рисунок 5.1 - Расчетная схема контура гидропривода

Основные допущения:

1. Свойства жидкости не изменяются в течение переходного процесса (температура, плотность, вязкость, количество нерастворённого воздуха);

2. Утечки жидкости в системе отсутствуют;

3.  моделируют напорный трубопровод;  – подводящий канал в распределителе. Причем воздействие задаём перемещением золотника распределителя  и моделируем его как типовую функцию;

4. Трением в цилиндре пренебрегаем.

На расчётной схеме гидроусилителя:

 перемещение столба жидкости;

 перемещение поршня цилиндра;

 сосредоточенная в трубопроводах масса жидкости;

эквивалентное сопротивление участка трубопровода;

длина трубопровода;

Кос – коэффициент обратной связи;

h(t) – перемещение золотника;

h(t)-закон входного воздействия, моделирующий перемещение золотника распределителя, зависящий от h(t) и Кос;

давление, создаваемое насосом;

 нагрузка на штоке цилиндра;

податливость жидкости.

Для описания динамики контура используют три группы уравнений:

1. Уравнение движения поршня.

Это уравнение отражает равновесие подвижных элементов под действием внешних сил:

                                                            (5.1)                                      

где   приведённая к поршню масса подвижных элементов;

 сумма активных сил, действующих на поршень;

 сумма сил сопротивления.

                                                (5.2)                                                       где   сила давления;

 площадь поршня.

                                                       (5.3)

где  суммарная сила трения:

           (5.4)

где  сила сухого трения;

 коэффициент вязкого трения.

 полезная нагрузка на штоке цилиндра:

                                                     (5.5)

где  постоянная нагрузка;

 коэффициент позиционной нагрузки.

Так как мы предположили, что трением в цилиндре можно пренебречь, то получим, что:

; уравнение движения поршня будет иметь вид:

                                                  (5.6)

2.Уравнение движения жидкости в трубопроводе (баланс давлений):

(5.7)

                                                        (5.8)

где потери по длине. Чтобы избежать разветвления вычислительного процесса при вычислении  для потерь по длине воспользуемся эмпирической непрерывной функцией:

                                          (5.9)

где   кинематическая вязкость, м²/с (  сСт);

 коэффициент, зависящий от шероховатости внутренних стенок трубопровода, ;

 плотность жидкости;

 скорость жидкости.

 потери на местные сопротивления:

,                                                        (5.10) где   коэффициент местного сопротивления.

 инерционные потери:

 .                                                           (5.11)

Подставляя эти уравнения, выражаем старшую производную:

                 (5.12)

Запишем уравнения движения жидкости для участков:

1) y2-y3:

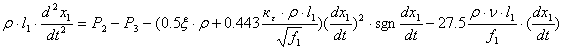или после преобразований

                           (5.13)

где 

Из (5.13) выразим :

           (5.14)

3.Уравнения расходов для узлов:

Для связи параметров движения жидкости на различных участках используют уравнения расходов. Эти уравнения составляются для узлов, выделенных на динамической схеме: . Для узлов, где учитывается сжимаемость жидкости , где  расход, затраченный на сжатие жидкости, сосредоточенной в узле.

1) Для узла :

(5.15)

                (5.16)

где   - коэффициент расхода распределителя;

 - диаметр золотника;

h(t) – закон входного воздействия;

K_oc – коэффициент обратной связи;

                                      (5.17)

                          (5.18)

Выразим из этого уравнения р₂:

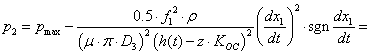
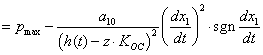
                                                        (5.19)

где .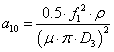

2) Для узла :

                                              (5.20)

                                            (5.21)

                                               (5.22)

                                              (5.23)

где  объем жидкости, сосредоточенной в узле;

 коэффициент податливости.

                                                         (5.24)

                              (5.25)

                                 (5.26)

где  базовый модуль упругости;

 расстояние между поршнем и крышкой в начальном положении;

 коэффициенты, учитывающие влияние давления и температуры;

 температура;

 базовая температура, при которой определяется ;

Слагаемое, учитывающее влияние температуры пренебрежимо мало, его можно не учитывать.  

 (5.27)         

         (5.28)

выразим из данного уравнения :

                            (5.29)

Подставив уравнение (5.19) в (5.13), получим:

       (5.30)

Таким образом, результирующая система (5.31) состоит из двух уравнений второго порядка (5.6) и (5.30) и 1-го уравнения первого порядка (5.29):

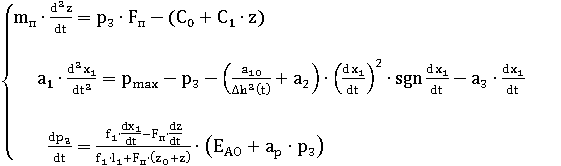   (5.31)

Систему (5.31) будем решать с помощью ЭВМ, используя метод Рунге-Кутта в соответствии с алгоритмом, схема которого представлена на рисунке 5.2. Так как метод Рунге-Кутта позволяет решать уравнения 1-го порядка, необходимо понизить порядок путем замены переменных. Путем понижения порядка она должна быть преобразована к системе состоящей из 5-ти уравнений.

Введем массивы функций и массивы производных (таблица 5.1):

Таблица 5.1 Массивы функций и производных                 

Перепишем уравнения с учетом принятых обозначений:

  

В таблице 5.2 представлены исходные данные для расчета:

По результатам расчета на ЭВМ строим графики переходного процесса представленные на рисунках 5.3, 5.4, 5.5.

По графику зависимости  определяем, что вид переходного процесса апериодический. Графическим методом определяем время переходного процесса. Время переходного процесса:

Результат динамического расчета:

t       hbx      z1      z1’       x1     x1’         P3

0.0000000 0.0000000000  0.00000  0.00000  0.00  0.00000    0.00000

0.1000000 0.0001629630  0.15999  1.85758  10.26  116.49983  0.48323

0.2000000 0.0003259259  0.33945  1.81431  21.79  113.90729  1.01145

0.3000000 0.0004888889  0.51368  1.70601  33.03  110.66651  1.53871

0.4000000 0.0006518519  0.68241  1.62717  43.93  107.34872  2.03830

1.0000000 0.0016296296  1.58032  1.34411  102.32  87.31902  4.71728

1.4400000 0.0022000000  2.11772  1.10354  137.53  72.75278  6.32045

1.4500000 0.0022000000  2.12877  1.10987  138.26  72.41980  6.35318

1.4600000 0.0022000000  2.13978  1.10386  138.98  72.09149  6.38507

1.5100000 0.0022000000  2.19400  1.07641  142.54  70.44299  6.54682

1.5500000 0.0022000000  2.23645  1.05836  145.33  69.12250  6.67442

1.5900000 0.0022000000  2.27809  1.02520  148.07  67.80842  6.79879

1.6000000 0.0022000000  2.28837  1.02764  148.75  67.47666  6.82965

Таблица 5.2 – Исходные данные для динамического расчета

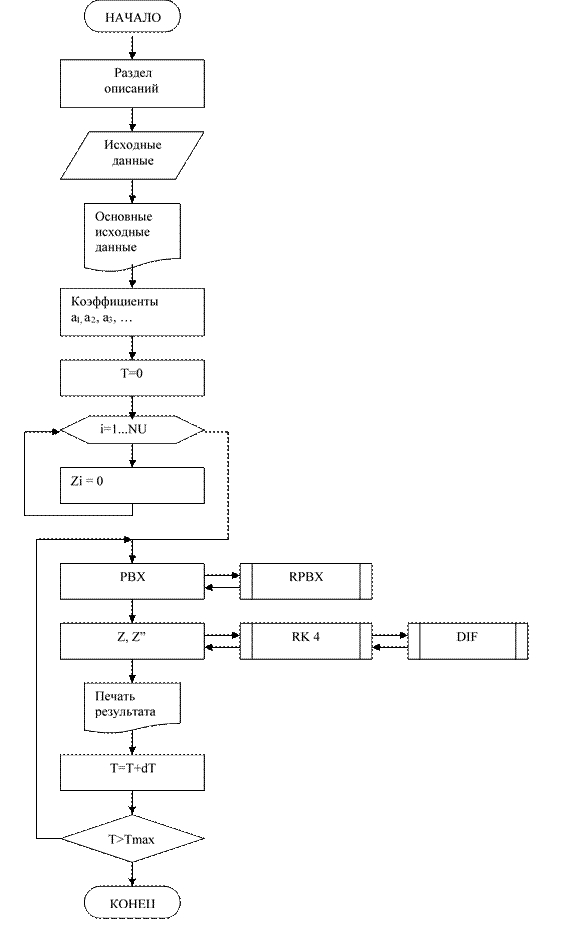
Рисунок 5.2. Схема алгоритма головной программы для решения д.у.

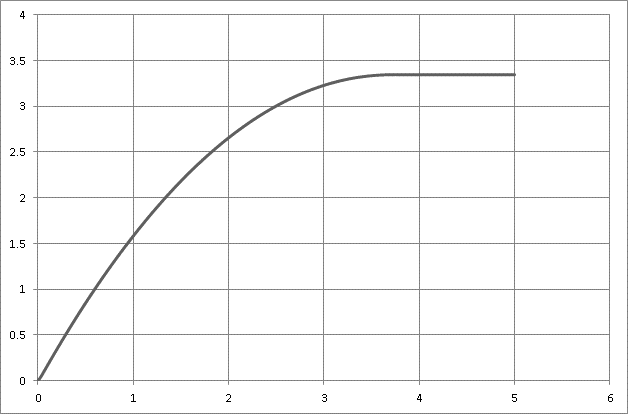
Рисунок 5.3 – График изменения перемещения поршня с течением времени

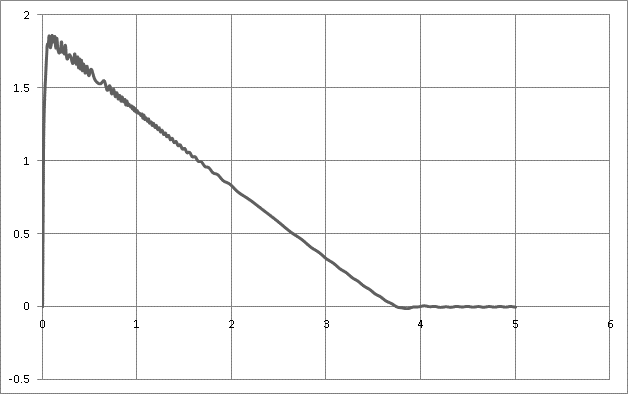
Рисунок 5.4 – График изменения скорости поршня с течением времени

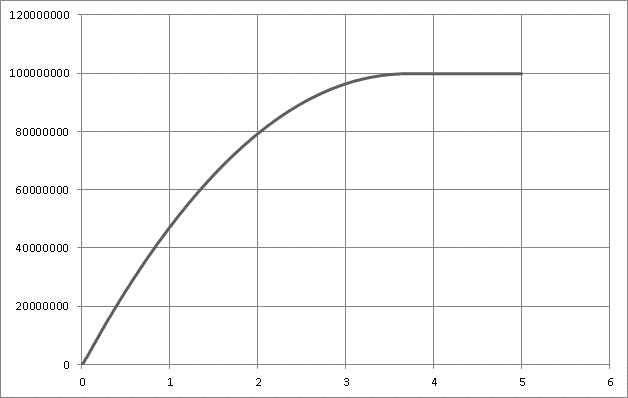
Рисунок 5.5 – График изменения давления

Таким образом, была разработана расчетная схема гидравлического контура и получена математическая модель, состоящая из пяти дифференциальных уравнений. С помощью ЭВМ методом Рунге-Кутта четвертого порядка была решена система уравнений и построены графики. В результате установлено, что система обладает устойчивыми параметрами