



МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Гидропневмоавтоматика и гидропневмопривод»
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №4
по дисциплине
«Теория автоматического управления»
Вариант 13/17
Выполнил:
гр. 101719
Проверил:
Минск 2012
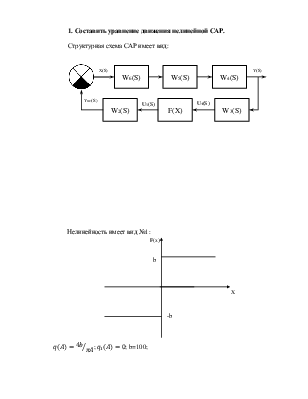
1. Составить уравнение движения нелинейной САР.
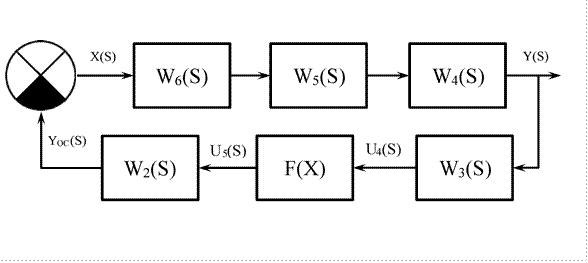
Структурная схема САР имеет вид:
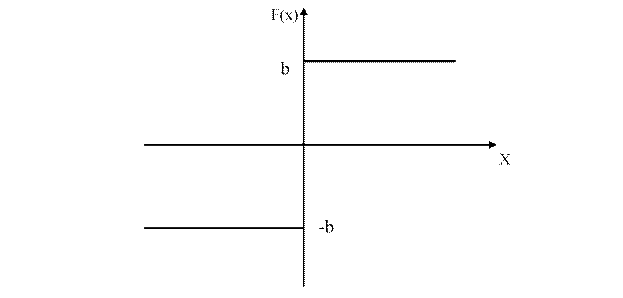
Нелинейность имеет вид №1:
![]() ;
; ![]() ; b=100;
; b=100;
По структурной схеме САР получаем уравнение движения линейной части:
![]()
![]()
![]()
![]()
Решим данные уравнения совместно и получим
Тогда уравнение движения линейной части имеет вид
Полученное уравнение является уравнением движения линейной части.
![]()
![]()
![]()
![]()
Данная нелинейность является однозначной.
![]() уравнение движения гармонически линеаризованного
нелинейного элемента.
уравнение движения гармонически линеаризованного
нелинейного элемента.
Запишем совместно уравнения движения линейной и нелинейной частей САР и получим:
Полученное уравнение является уравнением движения гармонически линеаризованной системы САР.
2. Найти параметры периодического движения системы.
Уравнение соответствует характеристическому уравнению:
Для отыскания существования периодического движения ![]() в
характеристический полином подставим
в
характеристический полином подставим![]() и
выделим вещественную и мнимую части:
и
выделим вещественную и мнимую части:
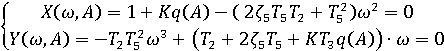
Из второго уравнения данной системы находим частоту периодического решения:
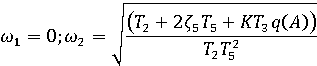
Подставив в первое уравнение системы ![]() , получим связь амплитуды и периода решения с
параметром системы:
, получим связь амплитуды и периода решения с
параметром системы:
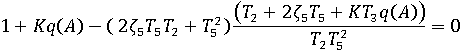
Найдём амплитуду автоколебаний из выражений и . Из после подстановки коэффициентов получим:
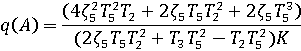
После подстановки всех коэффициентов, решаем это уравнение относительно А, и получаем:
Амплитуда автоколебаний равна ![]() 38240
38240
Из выражения найдём частоту автоколебаний:
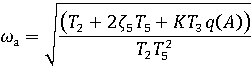
Частота автоколебаний равна ![]() 76,95 с-1
76,95 с-1
3. Для исследования устойчивости периодического решения воспользуемся алгебраическим критерием:
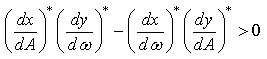
Тогда получим
Условие удовлетворяется, а следовательно,
найденное периодическое решение является устойчивым, а полученные параметры
являются параметрами автоколебаний, т.е ![]() 38240,
38240, ![]() 76,95 с-1
76,95 с-1
4. Определить частоту и амплитуду автоколебаний выходной величины y(t).
Частота автоколебаний ![]() остаётся неизменной для любой переменной системы,
а амплитуда преобразовывается линейной частью системы:
остаётся неизменной для любой переменной системы,
а амплитуда преобразовывается линейной частью системы:
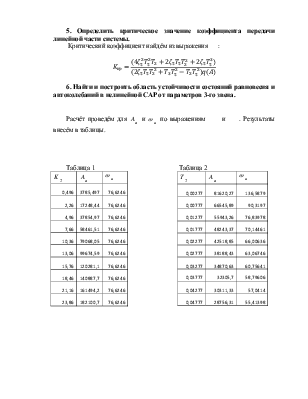
5. Определить критическое значение коэффициента передачи линейной части системы.
Критический коэффициент найдём из выражения :
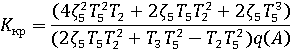
6. Найти и построить область устойчивости состояний равновесия и автоколебаний в нелинейной САР от параметров 3-го звена.
Расчёт проведём для ![]() и
и ![]() по выражениям и . Результаты внесём
в таблицы.
по выражениям и . Результаты внесём
в таблицы.
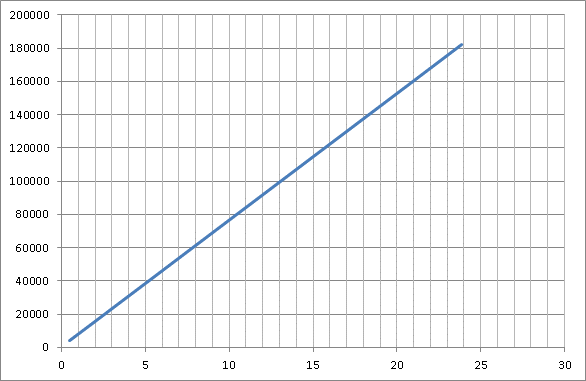
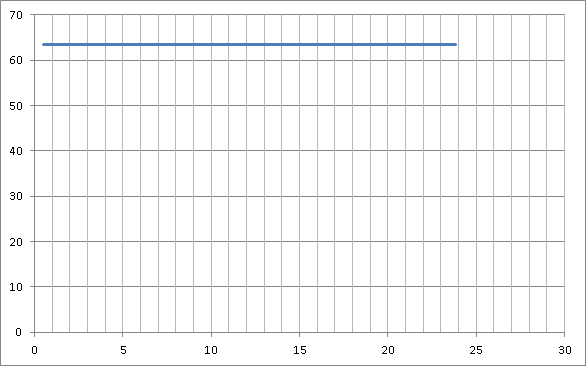
Таблица 1
|
|
|
|
|
0,496 |
3785,497 |
76,6246 |
|
2,26 |
17248,44 |
76,6246 |
|
4,96 |
37854,97 |
76,6246 |
|
7,66 |
58461,51 |
76,6246 |
|
10,36 |
79068,05 |
76,6246 |
|
13,06 |
99674,59 |
76,6246 |
|
15,76 |
120281,1 |
76,6246 |
|
18,46 |
140887,7 |
76,6246 |
|
21,16 |
161494,2 |
76,6246 |
|
23,86 |
182100,7 |
76,6246 |
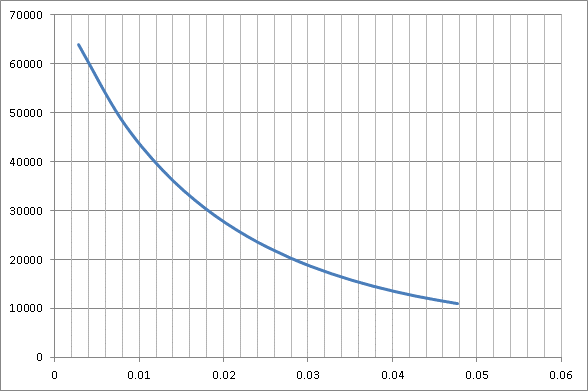
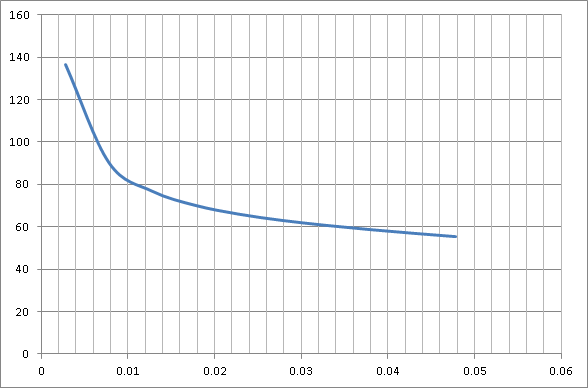
Таблица 2
|
|
|
|
|
0,00277 |
81620,27 |
136,5879 |
|
0,00777 |
66545,89 |
90,3197 |
|
0,01277 |
55943,26 |
76,83978 |
|
0,01777 |
48243,37 |
70,14461 |
|
0,02277 |
42518,85 |
66,00636 |
|
0,02777 |
38188,43 |
63,06746 |
|
0,03277 |
34870,63 |
60,75641 |
|
0,03777 |
32305,7 |
58,79606 |
|
0,04277 |
30311,33 |
57,0414 |
|
0,04777 |
28756,31 |
55,41398 |
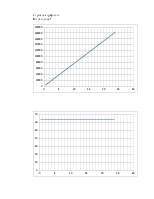
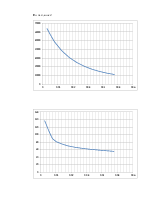
Строятся графики:
По таблице 1
По таблице 2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.