Закон больших чисел. Теорема Чебышева. Теорема Бернулли. Двумерные СВ. Функция распределения и её свойства

31. Закон больших чисел. Теорема Чебышева.

Нельзя заранее предвидеть какое из возможных значений примет СВ в итоге испыт. Это зависит от многих случайных причин, учесть которые невозможно.

Для оценки этих величин применяется теорема Чебышева и Бернулли.

Неравенство Чебышева:

X	x1	x2	…	xn
P	p1	p2	…	pn

Оценим отклонение СВ от её математического ожидания, и найдем при каких значениях это отклонение < ε

| ξ – М(ξ)| < ε                  если ε очень мало, ε0

ξ ~ M(ε)

Вероятность того, что отклонение СВ ξ от её математического ожидания по абсолютной величине < положительного числа ε, вероятность этого меньше, чем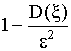 

p (| ξ – M (ξ)| < ε)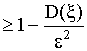

Доказательство:

Сущ. события

|ξ – M(ξ)| < ε  и |ξ – M(ξ)| ε

Сумма верностей этих сообщений равна 1.

p {|ξ – M (ξ)| < ε} + {|ξ – M (ξ)} ε|= 1

p {|ξ – M (ξ)| < ε} = 1- p {|ξ – M (ξ)|ε}

Найдем дисперсию

D(ξ)= [x₁-M(ξ)]² p₁+ [x₂- M (ξ)]² p₂+…+[x_n-M(ξ)]² p_n

[x_i – M(ξ)] < ε (k штук)        [x_j – M(ξ)] ε

D (ξ) [x_k+1 – M (ξ)]² p₁+…+ [x_n – M (ξ)]² p_n

|ξ – M (ξ)|ε –обе части положительные, возводим их в квадрат

|ξ – M (ξ)|²ε² , ε –уменьшится, неравенство усилится

D (ξ)ε² (p_k+1+p_k+2+…+p_n)

p {|ξ – M (ξ)|ε}

D (ξ) ε²     p {[ξ – M (ξ)] ε}

p {|ξ – M (ξ)| ε}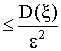

p {|ξ – M (ξ)| <ε}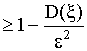

что и требовалось доказать.        

Теорема Чебышева.

Если x₁ , x₂ , … , x_n – это попарно независимый СВ причем дисперсии их равномерно ограничены и не превышают некоторые постоянные числа C (D(x_i))C,  i=, то каково бы ни было значение ε>0,неравенство

<ε

то вероятность неравенства равна 1, если число величин достаточно велико, т.е.             (1)

 

Доказательство:

среднее значение величины найдем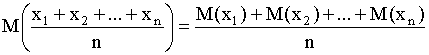 

p {|- M ()|<ε}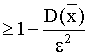

D () =

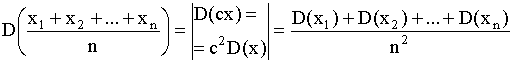
M (x_i) принимают значения 1-если соб. произ., 0-если не произ.

M (x₁) = 1p + 0q = p

D (x_i) c  

D ()

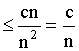
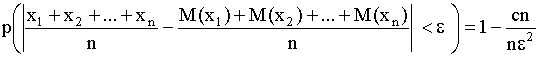
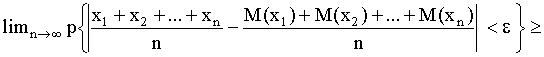
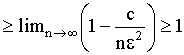
т.к. вероятность не может быть >1, то она  =1.

Следовательно (1) ч. и требовалось доказать.

Применяется в физике, когда большое число экспер.

32. Теорема Бернулли

Если в каждой из n испыт. вероятность появл. соб. A постоянна, то как угодно близка к един. вероятность того, что отклон. относ. частоты от вероятности испыт. по абсол. велич.будет сколь угодно мал, если число испыт. велико.

           

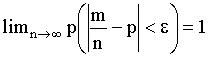
Доказательство:

x₁, x₂, …, x_n –дискр. СВ

M(x)=M(x₁)+M(x₂) +…+M(x_n)

M(x_i)=1p+0q=p

M(x_i²)=1²p+0²q=p

D(x_i)=M(x_i²)-[M(x_i)]²=p-p²=p(1-p)=pq

p+q=1;      p=;      q= --максимальное значение

D(x_i),     i=

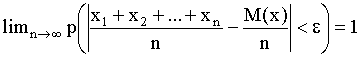
M(x₁)+M(x₂)+…+M(x_n)=M(x)

M(x)=np

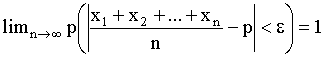
x₁+x₂+…+x_n=m

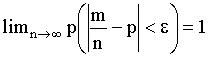
33. Двумерные СВ. Функция распределения и её свойства.

Двумерная случ. величина (x,y), если трёхмерная, то (x,y,z). Геометрически олредел. m или радиус --вектором OM

 

y                                              y                                                            

                                                                

      0                                x             0                                  x

З-ном распред-я двум СВ наз.перечень возможн. знач. этой велич., т.е. пар чисел (x_i, y_i) и их вероятность p' (x_i,y_i)

i=1,2,…,n          j=1,2,…,m

З-н распред-я в виде табл.

x y	x1	…	xi	…	xn
y1	p(x1,y1)	…	p(xi,y1)	…	p(xn,y1)
: :	: :	…	: :	…	: :
yj	p(x1,yj)	…	p(xi,yj)	…	p(xn,yj)
: :	: :	…	: :	…	: :
ym	p(x1,ym)	…	p(xi,ym)	…	p(xn,ym)

(X=x_i,Y=y_j)  i=;          j=

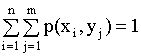
Т.к. можно рассм.  (x₁,y₁), …, (x₁,y_j), …, (y_m,x₁), то если возмем сумму

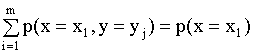
p(y=y_j)=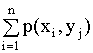

Функция распределения и её свойства.

,   

Функция распределения двум. СВ (x,y) наз. ф-ция F(x,y), определяющая для каждой пары чисел (x,y) вер-ть того, что X принимает значения < x, а Y-<y. Геометрически – это вер-ть того, что случ. m(x,y) попадает в  квадрат, располож. левее и ниже этой точки с вершиной (x,y)

Свойства функции распределения:

1. ф-ция удовлетвор. нер-ву

  это видно из опрдел.

2. ф-ция распредел. не убыв-ая ф-ии по своим составл. (по каждому аргум.), т.е.

3. имеет место предельное соотношение а)           б)

в)        г)

Док-во: а) , т.к. невозможное событие  т.е.

г)

4. при  ф-ция распред. системы станов. равной ф-ции распред. составл. x

аналог., если

Док-во: т.к. событие  достоверно, то вер-ть того, что , это и есть ф-ция распрдел. СВ

5. вер-ть попад. т. в полуполосу

6.вер-ть попадания в прямоугольник