Элементы теории временных рядов. Анализ временных рядов, страница 2

     у  временного ряда  случайная величина (признак) развивается во времени (значит могут меняться числовые характеристики).

2)  Члены временного ряда не являются одинаково распределенными.

      3)  Члены временных рядов  не являются статистически независимыми.

        Т.о. мы  не можем распространить свойства и правила статистического анализа случайной выборки на временной ряд.

       Однако, среди временных рядов есть такие, на которые мы может распространить часть этих свойств. Причем они представляют особый интерес и играют важное значение в  анализе  временных рядов. К таким рядам относятся  стационарные ряды, т.е. грубо говоря, ряды без тенденции. Стационарные временные ряды применяют при описании случайной компоненты  временного ряда.

       Определение. Под стационарным рядом ( в широком смысле) понимают временной ряд, у которого все характеристики не меняются с течением времени.

         К сожалению, наш математический аппарат не достаточен для понимания стационарного временного ряда в узком смысле.

         Под стационарными рядами в узком смысле понимают ряды, у которых законы распределения для

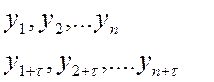 совпадаю,

где t - один и тот же временной сдвиг (лаг), причем t, n, t - любые.

        Свойства таких рядов не изменяются с изменением начала отсчета.

Характеристики временного  ряда:

 теоретические                          статистические

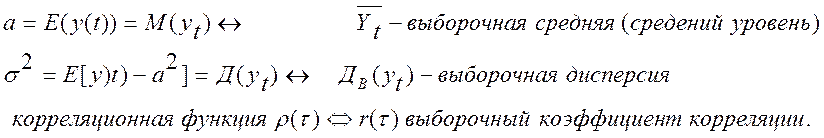
         Т.к. ряды стационарные и эти характеристики неизменны, то можно рассчитать их статистические аналоги (оценки)

         Вернемся, к примеру, № 1. (слайд)

                                                             

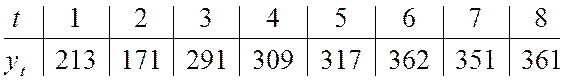
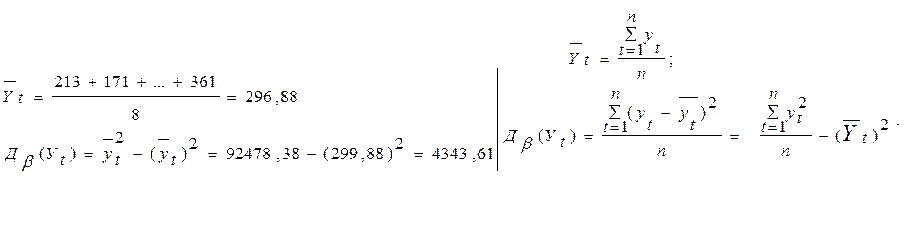
            Рассмотрим корреляционную функцию,  статистическим аналогом, которой будет коэффициент корреляции. Как известно из курса математической статистики, коэффициент корреляции характеризует  меру линейной зависимости между двумя случайными величинами.

Т.к. уровни временного ряда   не являются статистически независимыми, мы можем охарактеризовать меру этой зависимости.

Рассмотрим два ряда

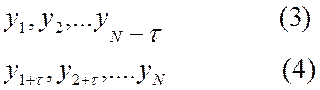, образованных из исходного (1), сдвигом на определенный промежуток времени   t, называемый лагом.

           Определение:  Под корреляционной функцией   понимают коэффициент корреляции  между уровнями .

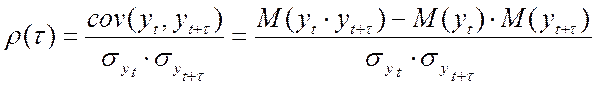
   Для стационарных ВР  ,

                                             

значит .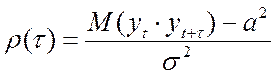

       Корреляционная функция показывает, как изменяется зависимость между уровнями с изменением временного промежутка.

        Замечание 1.  Для  стационарного ВР эта функция должна монотонно убывать.

        Замечание 2.   Т.к. корреляционная  функция характеризует зависимости между  уровнями одного и того же ряда, ее еще называют автокорреляционной функцией.

        Статистической оценкой этой величины является выборочный коэффициент автокорреляции  для временного лага t.

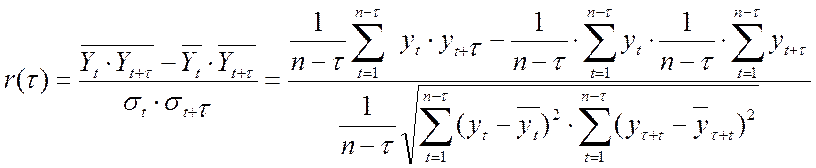
t  - называют порядком коэффициента корреляции.

В примере № 1  для расчета r(1) используют ряды:

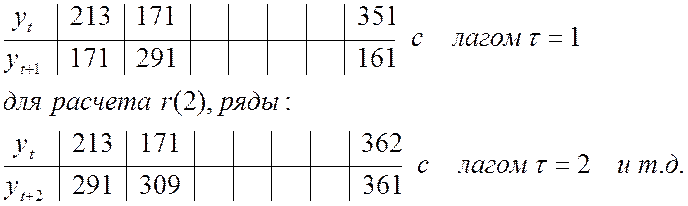
  Замечание 3.  С увеличением лага на единицу число пар значений анализируемых рядов уменьшается на единицу.

   Поэтому рекомендуют рассчитывать максимальный порядок выборочного коэффициента корреляции равный .

       Построение автокорреляционной функции бывает полезным для выявления структуры ВР  (т.е. состава компонент).

      При наличии во ВР трендовой и циклической компонент значения последующих уровней зависят от предыдущих.

       Если >, где ,, то ряд содержит только тренд.

       Если  наиболее высок, ¹1, то помимо тенденции в структуре ряда наблюдаются колебания с периодом t.

       В примере 1 рассчитаны коэффициенты корреляции 1-го, 2-го и 3-го порядка.

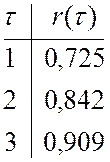
      Анализ.

3. Некоторые методы сглаживания временных рядов.

   Временной ряд можно разложить на  неслучайную и случайную компоненты.

^{символизирует}

^{основную тенденцию}

Определение: Выявление основной тенденции, выделение f(t) называют  выравниванием  (сглаживанием) временного ряда.

         Методы сглаживания делятся на:

1)   механические (без  количественной модели) [графические, метод скользящей  средней и т.д.]

2)   аналитические (с моделью) [подбор аналитической функции]

   В качестве тренда f(t) можно выбрать

    f(t) = a + вt – линейную модель

    f(t) = a + в₁× t+ в₂ × t² – квадратичную

    f(t) = e^a+вt – экспоненциальную.

    С подобным подбором сталкивались в лабораторной работе.

    Рассмотрим выделение линейного тренда в примере № 1.

    Будем полагать, что основная тенденция линейная, тогда

- модель нашего временного ряда.

    Осталось оценить параметры этой модели.

    Будем полагать, что  удовлетворяет условиям Гаусса-Маркова, тогда для оценки  а и в применим МНК.

      Система нормальных уравнений:

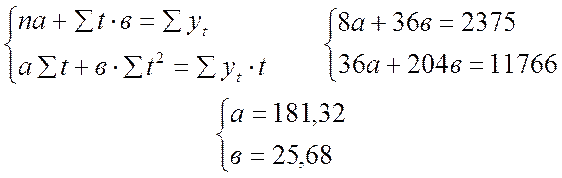     (слайд)

Уравнение трендовой модели  .

        Для оценки значимости модели используем критерий Фишера. F= 23,56, что гораздо больше F_{kp. Þ}  модель значима. Результаты аналитического сглаживания отражены на слайде.

        Рассмотрим один из методов механического сглаживания - метод  скользящей средней.

        Он  заключается в замене наблюдаемых значений уровней ВР средними значениями по какому-либо временному интервалу скольжения t.   При этом  сам ВР скользит по времени.

        В примере 1 средним значением по интервалу времени длиной t = 3:

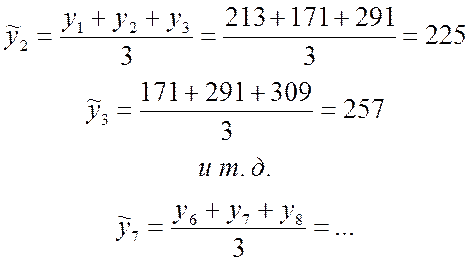
   Результаты сглаживания по методу скользящей средней отображены на слайде. (*)

                К сглаженным результатам гораздо проще подобрать аналитическую трендовую модель.

4.Понятие об  авторегрессионых моделях временных рядов.

        Когда  мы рассматривали способы выделения основной тенденции, предполагали, что выполняются условия Гаусса-Маркова, и метод НК применим для оценки параметров модели.

        Однако, чаще всего у ВР присутствует автокорреляция в остатках и использование  МНК для оценки параметров модели не подходит.

         В этом случае используют другую модель.

         Определение: Модель, в которой в качестве объясняющих (факторных) переменных используются значения результативной переменной, но в предыдущие моменты (так называемые лаговые значения), называется  моделью авторегрессии.

-  авторегрессионная модель порядка (глубины ) р.

        Наиболее прост частный случай при р =1

.

        Оценки параметров а и в₁  этой модели можно осуществить МНК, рассматривая в  качестве объясняющей переменной у_t, а  в качестве результативной

;   .                 

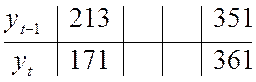        По этой модели можно осуществить прогноз, на недалеко вперед.

Заключение:

 Выводы по лекции.

      На лекции рассмотрен ряд понятий, являющихся ключевыми для анализа временных рядов:

 Временной ряды, компоненты временного ряда, характеристики временных рядов и их статистические аналоги. Сформулирована классическая задача статистического анализа временного ряда. Приведены примеры некоторых методов сглаживания временных рядов, построения простейшей линейной модели авторегрессии.