Исследование системы векторов на линейную зависимость. Определение координат вектора в базисе. Определение размерности линейного пространства решений системы

Координатные столбцы  – линейно независимы, следовательно, векторы  тоже линейно независимы и значит  – базис в линейном пространстве решений системы уравнений.

Найдем ранг матрицы системы

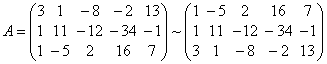
(поменяли местами первую и третью строки).

Вычтем элементы первой строки из соответствующих элементов второй строки, а затем элементы первой строки умножим на –3 и прибавим к элементам третьей строки, получим

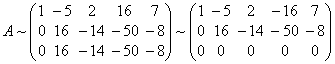
(при последнем преобразовании вычли элементы третьей строки из соответствующих элементов четвертой строки). Ранг матрицы системы равен двум, значит размерность пространства решений системы равна .

Исходная система равносильна системе

 ,

Полагая в этой системе сначала ; затем ; а потом , находим три линейно независимых решения:

а) ,

 ,      

б) ,

     ,   

в) ,

     ,   

,   ,   .

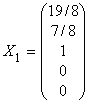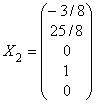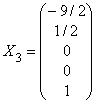Таким образом, базисом пространства решений будут, например, векторы:

,

здесь, для упрощения, координаты первых двух векторов умножены на 8, а координаты последнего – на 2.

Пример 8.4. Найти размерность и базис линейного подпространства, являющегося линейной оболочкой векторов.

Решение. Составим из координат векторов системы матрицу и с помощью элементарных преобразований определим ее ранг. Ранг этой матрицы будет совпадать с числом линейно независимых векторов в системе и значит, равен размерности оболочки векторов (см. раздел 1). Матрица из координат векторов имеет вид:

здесь, сначала элементы первой строки прибавили к соответствующим элементам второй и третьей строк, потом элементы первой строки умножили на два и прибавили к соответствующим элементам пятой строки, после чего элементы второй строки разделили на два и результат вычли из третьей, четвертой и пятой строк. Таким образом ранг матрицы равен двум, т.е. в системе два линейно независимых вектора, значит размерность линейной оболочки векторов равна двум. В качестве базиса можно взять, например векторы .

Пример 8.5. Пусть  Являются ли линейными следующие преобразования? 

Решение. Преобразование будет линейным, если все координаты образов векторов будут линейными комбинациями координат вектора . Здесь в преобразовании  вторая координата равная  не является линейной комбинацией, в преобразовании  - аналогично, кроме того третья координата имеет вид , что так же не является линейной комбинацией координат вектора . Значит эти преобразования не являются линейными. Преобразование  является линейным.

Пример 8.6. Найти матрицу линейного преобразования  в базисе  если она задана в базисе

 ,   .

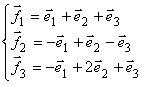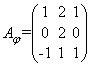Решение. При переходе от базиса  e  к базису  f матрица линейного преобразования, в соответствии с определением, будет иметь вид (см. (4.1))  , где  T  матрица перехода, которая находится из равенства  f = eT. Здесь .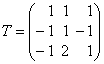

Найдем определитель матрицы: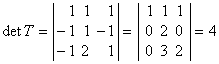 

(прибавили к элементам второй и третьей строк соответствующие элементы первой строки и записали формулу разложения определителя по первому столбцу).

Найдем алгебраические дополнения к элементам матрицы T и обратную матрицу по формуле :

.

Таким образом, обратная матрица будет 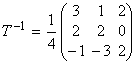  и, следовательно, 

.

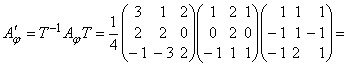
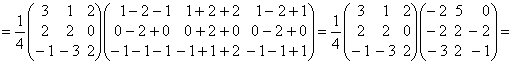
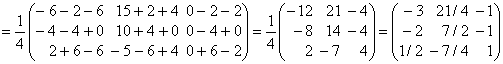Пример 8.7. Определить ранг и дефект линейного преобразования, а также найти базисы образа и ядра  при преобразовании .

.

Решение. Пусть в  выбран базис , тогда в этом базисе матрица преобразования  будет иметь вид:

.

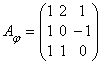По определению вектор  принадлежит образу  при преобразовании  в том и только том случае, когда найдется вектор  такой, что , или в координатной записи по формуле (3.4):

.

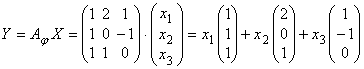Это равенство означает, что образ  совпадает с линейной оболочкой системы векторов , так как . Следовательно, ранг оператора , который совпадает с рангом его матрицы, равен двум. В качестве базиса можно взять любой базис линейной оболочки векторов , например,  – они линейно независимы.

Аналогично вектор  принадлежит ядру тогда и только тогда, когда , или, в координатной записи:

.

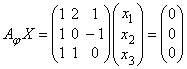Это однородная система линейных уравнений, ранг которой равен двум, значит, она эквивалентна следующей системе:

 , полагая в которой, например, , получаем , т.е. базис ядра состоит из одного вектора .

При этом по теореме 3.5, размерность ядра равна:

.

Пример 8.8. Доказать линейность, найти матрицу, область значений и ядро оператора:

а) проектирования на плоскость ;

б) зеркального отражения относительно плоскости .

Решение. Рассмотрим произвольный вектор . Отложим его от начала координат, тогда координаты точки конца вектора будут . Проекцию этого вектора на плоскость  обозначим , а зеркально отраженный