Анализ вариационных рядов. Выборочные наблюдения. Статистическое изучение корреляционных связей

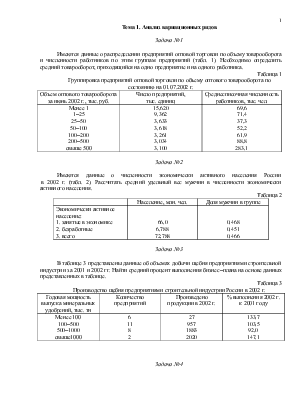
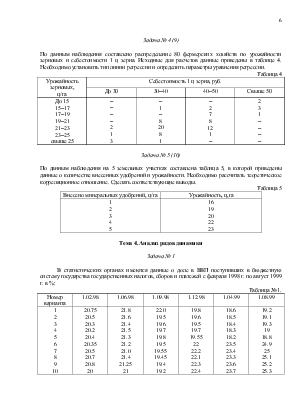
Бригада рабочих из шести человек занята штамповкой деталей. По данным в табл. 4 необходимо определить средние затраты времени на одну деталь.

Таблица 4

Индивидуальные затраты времени на изготовление деталей бригадой рабочих

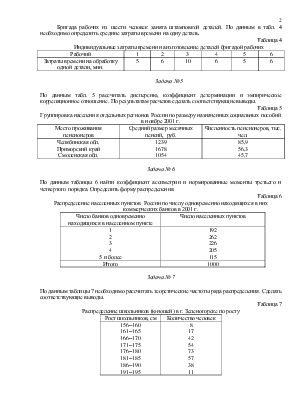
Задача № 5

По данным табл. 5 рассчитать дисперсию, коэффициент детерминации и эмпирическое корреляционное отношение. По результатам расчетов сделать соответствующие выводы.

Таблица 5

Группировка населения отдельных регионов России по размеру назначенных социальных пособий в ноябре 2001 г.

Задача № 6

По данным таблицы 6 найти коэффициент ассиметрии и нормированные моменты третьего и четвертого порядка. Определить форму распределения.

Таблица 6

Распределение населенных пунктов  России по числу одновременно находящихся в них коммерческих банков в 2001 г.

Задача № 7

По данным таблицы 7 необходимо рассчитать теоретические частоты ряда распределения. Сделать соответствующие выводы.

Таблица 7

Распределение школьников (юношей) в г. Зеленогорске по росту

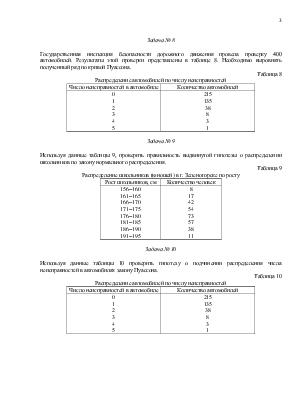
Задача № 8

Государственная инспекция безопасности дорожного движения провела проверку 400 автомобилей. Результаты этой проверки представлены в таблице 8. Необходимо выровнять полученный ряд по кривой Пуассона.

Таблица 8

Распределение автомобилей по числу неисправностей

Задача № 9

Используя данные таблицы 9, проверить правильность выдвинутой гипотезы о распределении школьников по закону нормального распределения.

Таблица 9

Распределение школьников (юношей) в г. Зеленогорске по росту

Задача № 10

Используя данные таблицы 10 проверить гипотезу о подчинении распределения числа неисправностей в автомобилях закону Пуассона.

Таблица 10

Распределение автомобилей по числу неисправностей

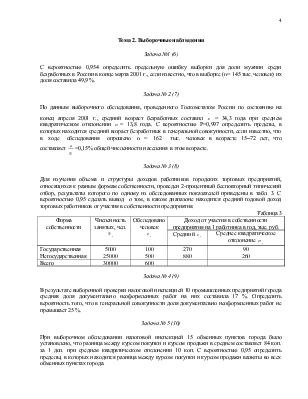
Тема 2. Выборочные наблюдения

Задача №1 (6)

С вероятностью 0,954 определить предельную ошибку выборки для доли мужчин среди безработных в России в конце марта 2001 г., если известно, что в выборке (n= 145 тыс. человек) их доля составила 49,9 %.

Задача № 2 (7)

По данным выборочного обследования, проведенного Госкомстатом России по состоянию на конец апреля 2001 г., средний возраст безработных составил  = 34,3 года при среднем квадратическом отклонении = 13,8 года. С вероятностью Р=0,997 определить пределы, в которых находится средний возраст безработных в генеральной совокупности, если известно, что в    ходе     обследования     опрошено    n   =    162      тыс.    человек   в   возрасте   15–72   лет,   что составляет =0,15% общей численности населения в этом возрасте.

Задача № 3 (8)

Для изучения объема и структуры доходов работников городских торговых предприятий, относящихся к разным формам собственности, проведен 2-процентный бесповторный типический отбор, результаты которого по одному из обследованных показателей приведены в табл. 3. С вероятностью 0,95 сделать вывод  о том, в каком диапазоне находится средний годовой доход торговых работников от участия в собственности предприятия.

Таблица 3

Задача № 4 (9)

В результате выборочной проверки налоговой инспекцией 10 промышленных предприятий города средняя доля документально неоформленных работ на них составила 17 %. Определить вероятность того, что в генеральной совокупности доля документально неоформленных работ не превышает 25 %.

Задача № 5 (10)

При выборочном обследовании налоговой инспекцией 15 обменных пунктов города было установлено, что разница между курсом покупки и курсом продажи в среднем составляет 84 коп. за 1 дол. при среднем квадратическом отклонении 10 коп. С вероятностью 0,95 определить пределы, в которых находится разница между курсом покупки и курсом продажи валюты во всех обменных пунктах города. 

Тема 3. Статистическое изучение корреляционных связей

Задача № 1 (6)

Имеются данные по 8 фирмам о часовой оплате труда х и уровне текучести кадров у (табл. 1). Необходимо измерить тесноту связи между х и у с использованием линейного коэффициента корреляции.

Таблица №1

Задача №2 (7)

По 10 фермерским хозяйствам имеются данные об урожайности картофеля у (ц/га) и о количестве внесенных на 1 га удобрений х (кг) (см табл. 2). Необходимо измерить тесноту связи между изменениями х и у с помощью коэффициентов корреляции Кендэла. 

Таблица 2

Задача № 3 (8)

По данным наблюдения на 5 земельных участках составлена таблица 3, в которой приведены данные о количестве внесенных удобрений и урожайности. Необходимо установить тип линии регрессии и определить параметры