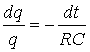Изучение процессов установления тока при разрядке и зарядке конденсатора, страница 2

                                                  .

Интегрирование дифференциального уравнения (2) приводит к выражению

,

где А – постоянная интегрирования.

  , ,

где q₀ и I₀ – первоначальные значения заряда и силы тока (ток в момент времени t = 0), а τ = RC – время релаксации.

2.  При зарядке конденсатора:

Заряд на обкладках конденсатора и зарядный ток в произвольный момент времени по определению равны

q = CU, .

   Из второго закона Кирхгофа имеем

RI + U = ε

где R – полное сопротивление цепи, включая внутренне сопротивление источника тока.

Продифференцировав и преобразовав данное уравнение получим:

.

Продифференцировав равенство по времени, найдем ток разрядки конденсатора

,

где I₀ – максимальное значение силы тока разрядки конденсатора в начальный момент времени t₀ = 0.

3.  Определение емкости и сопротивления в цепи зарядки и разрядки конденсатора:

Вычислим натуральный логарифм разрядного тока

.

Уравнение эквивалентно уравнению прямой. Если ввести обазначения y = lnI, a = lnI₀, , то получим

y = a + bx.

Из этой формулы можно найти значение lnI₀ и по его значению с помощью таблицы определяют начальное значение разрядного тока I₀ и вычисляют R и C по формулам