Определение точности изготовления деталей РЭС статистическим методом: Методические указания к лабораторной работе № 1 по дисциплине «Технология деталей РЭС», страница 4

В зависимости от формы кривой распределения вероятность получения брака определяется (в %) для двух случаев.

I. В случае смещения центра группировки от середины поля допуска на величину

                                                              (10)

Значение аргумента Z для верхнего (Z_в) и нижнего (Z_н) предельных значений допуска равно

,                                                        (11)

Вероятность получения брака α^' (в %) по верхнему предельному допуску равна

α^'_в = [0.5  - F(Z_в)]^.100%                                                        (12)

По нижнему пределу допуска –

α^'_н = [0.5 - F(Z_н)]^.100%                                                         (13)

2. Для случая совмещения поля рассеивания с серединой поля допуска (по абсциссе) вероятность получения брака (в %) равна

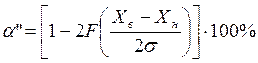                                               (14)

Указанная методика определения брака на основе применения закона  нормального распределения справедлива при объеме партии деталей не менее 100 штук. При  объеме партии  n≥50 погрешность определения брака изменяется на незначительную величину, а при партии n<50 погрешность возрастает. В этом случае более точные значения дает t-распределение Стьюдента (приложение 2).                    

В таблице всякому фиксированному значению объема партии деталей nесть три значения параметра  t, каждое из которых соответствует определенной вероятности Р(t)(0.95; 0.99; 0.999). Значение параметра t определяется по формулам (11), приняв значение σ равное среднеквадратичному отклонению для заданной  партии деталей, меньшей 100. Вычислив параметр t, по таблице приложения 2, находится Р(t) при заданном значении объеме n партии деталей и затем по формулам (12 - 14) определяется вероятность получения брака, при этом в формулах  вместо F(Z) подставляется 1/2 P(t).

3. ВОПРОСЫ К ДОМАШНЕМУ ЗАДАНИЮ

1. В чем заключается сущность обработки деталей на токарных станках ?

2. Какие бывают погрешности при обработке деталей резанием?

3. Причины возникновения систематических погрешностей при обработке деталей резанием.

4. .Причины возникновения случайных погрешностей при обработке деталей резанием.

5. Как влияют систематические и случайные погрешности на точность обработки?

4. ЛАБОРАТОРНЫЕ ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИХ  ВЫПОЛНЕНИЮ

Задание первое. Определить статистические параметры и точность обработки.

Методические указания по выполнению первого задания.

Получить у лаборанта набор деталей, изготовленных методом точения, измерительный инструмент и произвести измерения партии деталей с точностью не ниже 0,01 мм. Затем заполнить статистическую таблицу, для чего все полученные размеры разбить на интервалы и определить среднеарифметическое значение в интервалах, число показаний в каждом интервале. После произведенных расчетов определяется вероятность попадания в каждом интервале и рассчитываются среднеарифметическое и среднеквадратичное значения всей совокупности деталей. Строится кривая фактического распределения размеров (гистограмма и полигон). Полученные значения практического рассеивания сравниваются с допуском на размер детали по чертежу. Условием обработки деталей без брака является

6σ ≤ δ, где  σ - допуск на размер детали по чертежу.

Если 6σ ≥ δ, то брак в обработке деталей недопустимо велик.

Задание второе. Построить теоретическую кривую нормального распределения, совместить ее с фактической кривой распределения и определить вероятность выхода годных деталей.

Методические указания по выполнению второго задания