Основными характеристиками распределения являются:
среднее значение размеров обрабатываемой детали и мера рассеивания погрешности
обработки. В качестве средних значений размеров используется
среднеарифметическое значение ![]() .
Если изготовлено n деталей, то в этом случае весь диапазон измеренных
значений xi разбивается на N интервалов, ширина интервала равна
.
Если изготовлено n деталей, то в этом случае весь диапазон измеренных
значений xi разбивается на N интервалов, ширина интервала равна
![]() , где
, где ![]() . Тогда
. Тогда ![]() можно
определить из выражения
можно
определить из выражения
![]()
![]() (1)
(1)
где mi – количество деталей, попавших в данный интервал;
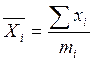 –
среднее значение в интервале (xi –
размеры деталей, попавших в данный интервал);
–
среднее значение в интервале (xi –
размеры деталей, попавших в данный интервал);
![]() – вероятность
появления величины в данном интервале (частоты).
– вероятность
появления величины в данном интервале (частоты).
При механической обработке систематические погрешности влияют на среднеарифметическое значение (центр группирования размеров) обрабатываемых деталей.
Для характеристики рассеивания случайных погрешностей наиболее употребительным является среднее квадратичное отклонение σ, которое определяется как корень квадратный из дисперсии.
Дисперсией дискретной случайной величины называется сумма квадратов отклонения случайной величины Xi от ее среднего значения, поделенная на число измерений:
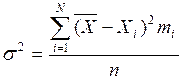 или
или ![]() .Ошибка! Объект не может быть создан
из кодов полей редактирования.
(2)
.Ошибка! Объект не может быть создан
из кодов полей редактирования.
(2)
Отклонение действительных размеров годных деталей от среднего размера всей обработанной партии деталей согласно закону 3σ /1/ должно находиться в пределах от – 3σ до + 3σ. Практически с погрешностью 0,27% можно считать, что в пределах ±3σ заключены все размеры деталей, годных для использования в каких-либо конструкциях.
Установлено /I/, что при обработке деталей резанием распределение погрешностей, вызванных действием случайных факторов, лучше всего описывается законом нормального распределения или кривой Гаусса.
Общее уравнение кривой нормального распределения имеет вид
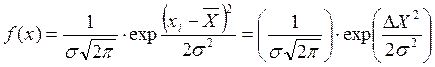 (3)
(3)
где xi – размер деталей;
![]() – среднеарифметический размер;
– среднеарифметический размер;
σ – среднее квадратичное отклонение;
![]() –
отклонение фактических размеров от среднеарифметического.
–
отклонение фактических размеров от среднеарифметического.
Для упрощенного построения кривой нормального распределения достаточно определить σ и знать три параметра:
1. Максимальную ординату Ymax (при ∆X = 0)
![]() .
(4)
.
(4)
2. Ординаты в точках перегиба Yn при X = ± σ
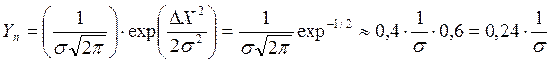 . (5)
. (5)
3. Величину поля рассеивания (поля допуска)
Yp = 0.0027 при ∆X = δ = ± 3σ . (6)
Для сравнения теоретической кривой нормального распределения с фактической кривой распределения необходимо по данным замеров деталей построить гистограмму. Для этого полученный ряд результатов измерений необходимо разбить на N равных интервалов и определить частоты попадания размеров (mi) в каждый интервал. Полученные данные заносятся в табл.1.
Таблица 1
|
Интервалы |
xi |
Сводка mi |
|
|
|
|
|
|
1 |
|||||||
|
2 |
|||||||
|
3 |
|||||||
|
… |
|||||||
|
N |
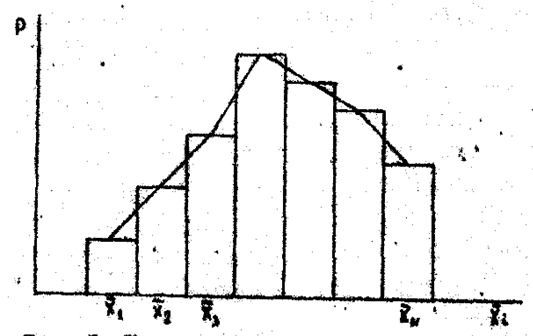
Для графического построения распределения размеров по
оси абсцисс откладывают установленные размеры интервалов, а по оси ординат –
вероятности ![]() (рис
1).
(рис
1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.