Определение точности изготовления деталей РЭС статистическим методом: Методические указания к лабораторной работе № 1 по дисциплине «Технология деталей РЭС», страница 3

Рис.1.  Кривая фактического распределения размеров при обработке деталей резанием

Полученный ступенчатый график называется гистограммой распределения, площадь каждого прямоугольника пропорциональна вероятности или частоте появления размеров. Соединив прямыми отрезками середины верхних сторон прямоугольников гистограммы, получим ломаную кривую, называемую эмпирической кривой распределения (полигоном).

Для сравнения теоретической кривой нормального распределения и эмпирической необходимо начертить их в совмещенных масштабах (рис.2). Для этого необходимо вычисленные ординаты теоретической кривой нормального распределения умножить на величину интервала полученных размеров  (∆Х)  и на  полное число  деталей в партии (n). Расчетные  формулы  кривой нормального распределения примут вид     (при X=0),

   (при Х = ±σ)                                                 (7)

Полученные точки соединяются плавной кривой. В точках  ±3σ величина поля рассеяния асимптотически приближается к оси абсцисс (P_i  = 0,0027).

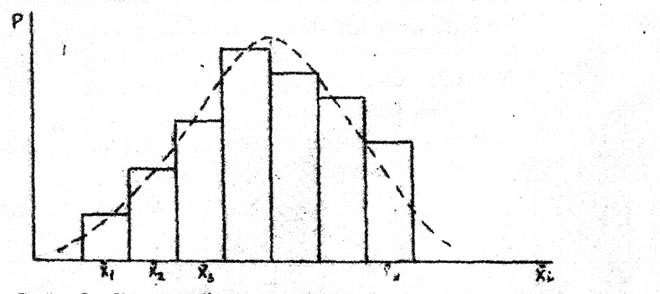
Рис.2. Кривая фактического распределения размеров и кривая нормального распределения

Закон нормального распределения оказывается справедлив при обработке деталей резанием при квалитетах точности 10 - 12 и грубее.

Полученные значения практического рассеивания сравниваются с допуском на размер детали по чертежу. Условием обработки деталей без брака является

6σ ≤ δ, где δ – допуск на размер по чертежу.

Если условие равенства выполняется, то точность обработки считается удовлетворительной. Это условие является необходимым, но недостаточным, т.к. возможен брак даже при выполнении неравенства 6σ ≤ δ,если настройка станка выполнена с некоторой погрешностью, превышающей допустимую.

В случае, если  6σ ≥ δ, то брак обработки деталей недопустимо велик.

Задание № 2. Изучить методику определения вероятностного выхода годных деталей.

Методические указания по выполнению второго задания

При выполнении второго задания изучить материал /I, с.22-24/.

На основании полученной кривой распределения размеров можно найти вероятное количество годных деталей, на размер которых установлен определенный допуск. Поле допуска устанавливается размерами   X_в и Х_н   границ этого допуска от центра группирования. Вероятное количество годных деталей определяется в этом случае отношением заштрихованной площади    F1+F2 ко всей площади, заключенной между кривой и осью абсцисс (рис. 3).

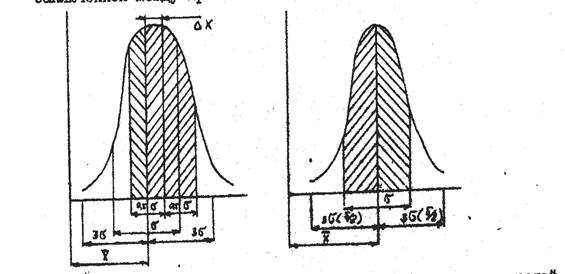
Рис 3. Определение вероятного количества годных деталей

С уменьшением допуска отношение площадей уменьшается и падает вероятное количество годных деталей. При значительном расширении поля допуска отношение площадей приближается к 1.

При симметричном расположении ноля рассеивания относительно поля допуска можно найти удвоенное значение интеграла, определяющего половину площади, ограниченной кривой Гаусса и  осью абсцисс.

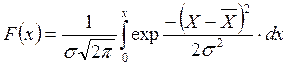                                                                   (8)

Затем после преобразования это выражение приводит к форме известной функции Лапласа

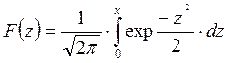                                                               (9)

где  .

Решение функции Лапласа не зависит от конкретных значений б и Х₀, а полностью определяется отношением

 , где F от Z – табличные значения.

Определение количества деталей, изготовленных без брака, сводится к установлению величины Z и определению по таблице значения F(z)  (см. приложение I), которое пересчитывается в % или в число штук деталей. Определив вероятность получения годных деталей в пределах поля допуска, можно определить вероятность получения разметов деталей, выходящих за пределы (верхний и нижний) поля допуска, т.е. вероятность получения брака.